算法的时间复杂度是什么

算法的时间复杂度的意思是:
算法的时间复杂度是衡量一个算法效率的基本方法。在阅读其他算法教程书的时候,对于算法的时间复杂度的讲解不免有些生涩,难以理解。进而无法在实际应用中很好的对算法进行衡量。
《大话数据结构》一书在一开始也针对算法的时间复杂度进行了说明。这里的讲解就非常明确,言简意赅,很容易理解。下面通过《大话数据结构》阅读笔记的方式,通过原因该书的一些简单的例子和说明来解释一下算法的时间复杂度和它的计算方法。
算法的时间复杂度是什么的函数
算法的时间复杂度,是一个用于度量一个算法的运算时间的一个描述,本质是一个函数。
根据这个函数能在不用具体的测试数据来测试的情况下,粗略地估计算法的执行效率,换句话讲时间复杂度表示的只是代码执行时间随数据规模增长的变化趋势。
常用大O来表述,这个函数描述了算法执行所要时间的增长速度,记作f(n)。算法需要执行的运算次数(用函数表示)记作T(n)。存在常数 c 和函数 f(n),使得当 n >= c 时 T(n) <= f(n),记作 T(n) = O(f(n)),其中,n代表数据规模也就是输入的数据。
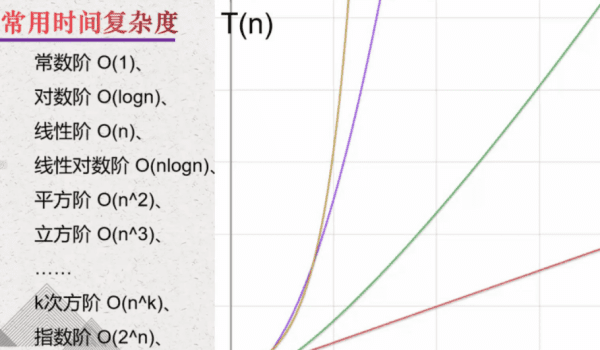
时间复杂度如何计算
1、常量阶:只要代码的执行时间不随 n 的增大而增长,这样代码的时间复杂度都记作 O(1)。或者说,一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)。
2、线性阶、n方阶:一般情况下,如果循环体内循环控制变量为线性增长,那么包含该循环的算法的时间复杂度为O(n),线性阶嵌套线性阶的算法时间复杂度为O(nⁿ),涉及下文乘法法则。
3、线性对数阶:当一个线性阶代码段法嵌套一个对数阶代码段,该算法的时间复杂度为O(nlogn)。
4、指数阶和阶乘阶:根据函数,随着n的增加,运行时间会无限急剧增加,因此效率非常低下。
计算机算法的时间复杂度是指什么
算法的时间复杂度是指:执行程序所需的时间。
一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近无穷大时。
T(n)/f(n)的极限值为不等于零的常数,则称为f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n))为算法的渐进时间复杂度,简称时间复杂度。比如:
在 T(n)=4nn-2n+2 中,就有f(n)=nn,使得T(n)/f(n)的极限值为4,那么O(f(n)),也就是时间复杂度为O(n*n)。
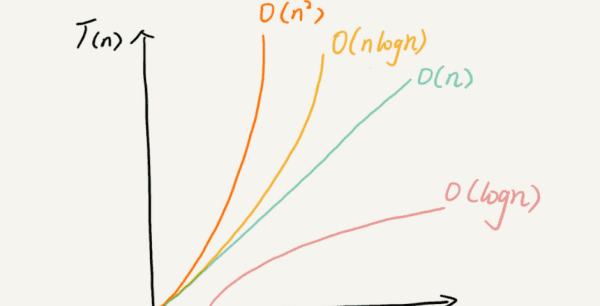
时间复杂度中大O阶推导是:
推导大O阶就是将算法的所有步骤转换为代数项,然后排除不会对问题的整体复杂度产生较大影响的较低阶常数和系数。
有条理的说,推导大O阶,按照下面的三个规则来推导,得到的结果就是大O表示法:运行时间中所有的加减法常数用常数1代替。只保留最高阶项去除最高项常数。
其他常见复杂度是:
f(n)=nlogn时,时间复杂度为O(nlogn),可以称为nlogn阶。
f(n)=n³时,时间复杂度为O(n³),可以称为立方阶。
f(n)=2ⁿ时,时间复杂度为O(2ⁿ),可以称为指数阶。
f(n)=n!时,时间复杂度为O(n!),可以称为阶乘阶。
f(n)=(√n时,时间复杂度为O(√n),可以称为平方根阶。
算法的时间复杂度指的是什么
时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐进的,亦即考察输入值大小趋近无穷时的情况。
空间复杂性介绍
空间复杂性是指计算所需的存储单元数量。隶属于计算复杂性(计算复杂性由空间复杂性和时间复杂性两部分组成)。算法的复杂性是算法运行所需要的计算机资源的量,需要时间资源量称为时间复杂性,需要空间资源的量成为空间复杂性。
一个算法的空间复杂度S(n)定义为该算法所耗费的存储空间,它也是问题规模n的函数。渐近空间复杂度也常常简称为空间复杂度。算法的时间复杂度和空间复杂度合称为算法的复杂度。
算法的时间复杂度是什么意思
执行一个算法所耗费的时间,从理论上是不能算出来的,必须上机运行测试才能知道。但不可能也没有必要对每个算法都上机测试,只需知道哪个算法花费的时间多,哪个算法花费的时间少就可以了。一个算法花费的时间与算法中语句的执行次数成正比例,算法中哪个语句的执行次数多,它花费的时间就多。
1.语句频度在算法中一个语句的执行次数称为语句频度或时间频度,记为T(n)。
2)算法的渐进时间复杂度一般情况下,算法的执行时间T是问题规模n的函数,记作T(n)。要精确地表示算法的运行时间函数常常是很困难的,即使能够给出,也可能是个相当复杂的函数,函数的求解本身也是相当复杂的。为了客观地反映一个算法的执行时间,可以用算法中基本语句的执行次数的数量级来度量算法的工作量,称作算法的渐进时间复杂度,简称时间复杂度,通常用O来表示。
算法的基本概念是什么算法复杂度的概念和意义
算法是指按照一定规则解决某一类问题的明确和有限的步骤。 算法复杂度主要表现为时间复杂度和空间复杂度,同一算法其复杂度将直接影响其算法乃至程序的优劣。一般来说,算法的复杂度越低,其效率就越高。算法复杂度是衡量程序优劣及效率的重要指标。
算法的复杂度和时间复杂度的关系
对于一个算法,其时间复杂度和空间复杂度往往是相互影响的。当追求一个较好的时间复杂度时,可能会使空间复杂度的性能变差,即可能导致占用较多的存储空间;反之,求一个较好的空间复杂度时,可能会使时间复杂度的性能变差,即可能导致占用较长的运行时间。
另外,算法的所有性能之间都存在着或多或少的相互影响。因此,当设计一个算法(特别是大型算法)时,要综合考虑算法的各项性能,算法的使用频率,算法处理的数据量的大小,算法描述语言的特性,算法运行的机器系统环境等各方面因素,才能够设计出比较好的算法。
优先时间复杂度的算法
时间复杂度是一个算法流程中,最差情况下常数操作数量的指标。
例子:一个有序数组A,另一个无序数组B,请打印B中所有不在A中的数。A数组长度为N,B数组长度为M。
第一种方法:B中每个数在A中遍历一下,输出所有不在A中的数。
A = list(map(int,input().split()))
B = list(map(int,input().split()))
N = len(A)
M = len(B)
for i in range(M):
j = 0
while j<N and B[i]!=A[j]:
j += 1
if j==N:
print(B[i])
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
第一种方法包含两个循环,对B遍历一遍,B中每个数又要在A中遍历一遍,因此时间复杂度为O ( M × N ) O(M\times N)O(M×N)。
第二种方法:B中每个数在A中二分找一下。
因A有序(假设升序),将A进行二分,分为left和right。中间位置的数为mid。将B中每个数先与mid相比较,如果B[i]比mid大,那么B[i]只可能在A的right,如果B[i]比mid小,那么B[i]只可能在left。每次砍一半的操作,时间复杂度为O ( log 2 N ) O(\log_2N)O(log
2
N),又对B中每个数遍历一次,故这个算法的时间复杂度为M × O ( log 2 N ) M\times O(\log_2N)M×O(log
2
N)。
二分法的停止条件是左边界超过右边界,while L<=R,也不用担心mid在加加减减过程中越界。
A = list(map(int,input().split()))
B = list(map(int,input().split()))
N = len(A)
M = len(B)
def binSearch(A,b):
L = 0
R = len(A)-1
while L<=R:
mid = int((L+R)/2)
# 在A中找到b了,返回True
if b==A[mid]:
return True
# b比A[mid]小,说明b在左边
if b<A[mid]:
R = mid - 1
# b比A[mid]大,说明b在右边
if b>A[mid]:
L = mid + 1
# 没找到b,返回False
return False
for i in range(M):
flag = binSearch(A,B[i])
if not flag:
print(B[i])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
第三种方法:先给B排序,然后用类似外排的方法打印不在A中的数。
关于排序算法之后单独介绍,对B排序后,在A,B均为有序数组。
在这里插入图片描述
a指针指向1,b指针指向3,当a<b时,a只能往后移动,当a=b时,b只能往后移动,当a>b时,打印b,同时b往后移。
(1)排序代价O ( M × log M ) O(M\times\log M)O(M×logM) (2)打印数过程中,a最多指N NN个数,b最多指M MM个数,所以时间复杂度O ( N + M ) O(N+M)O(N+M)
因此整个算法时间复杂度O ( M × log M ) + O ( N + M ) O(M\times\log M)+O(N+M)O(M×logM)+O(N+M) 。
停止条件是A或B数组已经到界了,如果A到界了,那么B[b,M-1]均需打印出来;如果B到界了,说明B数组里的数已经查找完了。
A = list(map(int,input().split()))
B = list(map(int,input().split()))
N = len(A)
M = len(B)
a = b = 0
while a<N and b<M:
if A[a]<B[b]:
a += 1
elif A[a]==B[b]:
b += 1
else:
print(B[b])
b += 1
while b<M:
print(B[b])
b += 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
排序算法
冒泡排序
算法思想:从小到大排。每次找到最大的数放在末位。
第一次看0,1位置比较大小,0位置比1位置大就交换。
第二次看1,2位置比较大小,1位置比2位置大就交换,依次进行下去,第一次遍历,最大的数会被排到最后。
第二次只需遍历0至end-1个数,因为最大的数已经到最后,然后重复第一步步骤,直到所有数被排好。
def BubbleSort(arr):
length = len(arr)
if not arr or length < 2:
return arr
for i in range(length,-1,-1):
for j in range(0,i-1):
if arr[j] > arr[j+1]:
tmp = arr[j]
arr[j] = arr[j+1]
arr[j+1] = tmp
return arr
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
常数操作次数为N + ( N − 1 ) + ( N − 2 ) + ⋯ + 2 + 1 N+(N-1)+(N-2)+\cdots+2+1N+(N−1)+(N−2)+⋯+2+1,所以算法时间复杂度为O ( N 2 ) O(N^2)O(N
2
)。
选择排序
算法思想:从小到大排。
第一步,从0到N-1位置找到最小的数放在[0]位置上。
第二步,从1到N-1位置找到最小的数放在[1]位置上。
…
如何确定最小的数? 先找一个基准数,比基准数小的就互换,成为新的基准数。
def SelectionSort(arr):
length = len(arr)
if not arr or length < 2:
return arr
for i in range(length):
minNumber = arr[i]
for j in range(i+1,length):
if minNumber > arr[j]:
tmp = minNumber
minNumber = arr[j]
arr[j] = tmp
arr[i] = minNumber
return arr
1
2
3
4
5
6
7
8
9
10
11
12
13
1
2
3
4
5
6
7
8
9
10
11
12
13
算法时间复杂度为O ( N 2 ) O(N^2)O(N
2
)。
插入排序
算法思想:从小到大排。
每进来一个数,与它前面一个数比较,比前面的数小就交换,到了前一个位置后,在与前前位置的数比较大小,小就交换,大就停止。再进来一个数,按照上面的方法与前面的数交换插入。
def InsertSort(arr):
length = len(arr)
if not arr or length < 2:
return arr
for i in range(1,length):
j = i - 1
while j>=0:
if arr[j] > arr[j+1]:
tmp = arr[j]
arr[j] = arr[j+1]
arr[j+1] = tmp
j -= 1
else:
j = -1
return arr
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
插入排序的时间复杂度与数据状况有关。例如数组[1,2,3,4,5]整体有序,那么在计算时代价为O ( N ) O(N)O(N),但如果是[5,4,3,2,1]要升序排列,那么代价就是O ( N 2 ) O(N^2)O(N
2
),按最差情况计算,所以插入排序算法时间复杂度为O ( N 2 ) O(N^2)O(N
2
)。
归并排序
算法思想:将数组一分为二,分别把左侧和右侧部分排好序,然后再利用外排的方式将整体排好序。
左右排好序后,需要一个辅助数组,左右两边比较大小,将小的数依次填入辅助数组。额外空间复杂度为O(n)。
def MergeSort(arr):
length = len(arr)
if not arr or length < 2:
return arr
sortProcess(arr,0,length-1)
return arr
def sortProcess(arr,L,R):
if L==R:
return arr[L]
mid = (L+R)//2
sortProcess(arr,L,mid)
sortProcess(arr,mid+1,R)
merge(arr,L,mid,R)
def merge(arr,L,mid,R):
help = []
p1 = L
p2 = mid+1
while p1<=mid and p2<=R:
if arr[p1] < arr[p2]:
help.append(arr[p1])
p1 += 1
else:
help.append(arr[p2])
p2 += 1
while p1<=mid:
help.append(arr[p1])
p1 += 1
while p2<=R:
help.append(arr[p2])
p2 += 1
for i in range(len(help)):
arr[L+i] = help[i]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
递过算法的时间复杂度计算有一个master公式:
T ( N ) = a × T ( N b ) + O ( N d ) T(N)=a\times T(\frac{N}{b})+O(N^d)
T(N)=a×T(
b
N
)+O(N
d
)
N b \frac{N}{b}
b
N
表示子过程的规模,a aa表示子过程的个数,O ( N d ) O(N^d)O(N
d
)表示除去调用子过程之外,剩余操作的时间复杂度。
当log b a > d \log_ba>dlog
b
a>d时,算法复杂度为O ( N log b a ) O(N^{\log_ba})O(N
log
b
a
)
当log b a = d \log_ba=dlog
b
a=d时,算法复杂度为O ( N d × log N ) O(N^d\times\log N)O(N
d
×logN)
当log b a < d \log_ba<dlog
b
a<d时,算法复杂度为O ( N d ) O(N^d)O(N
d
)
归并排序将数据规模一分为二,分为左右两个子过程,即a = 2 , b = 2 a=2,b=2a=2,b=2,且外排时间复杂度为O ( N ) O(N)O(N),d = 1 d=1d=1,所以为第二种情况。归并算法的时间复杂度为O ( N × log N ) O(N\times\log N)O(N×logN)。
以上就是关于算法的时间复杂度是什么的全部内容,以及算法的时间复杂度是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。










