自然底数e等于多少
1、e是自然对数的底数,是一个无限不循环小数,其值是2.71828……。对于数列{(1+1/n)^n},当n趋于正无穷时该数列所取得的极限就是e,即e=lim(1+1/n)^n。通过二项式展开,取其部分和,可得e的近似计算式e=1+1+1/2!+1/3!+1/4!+...+1/n!n越大,越接近的真值。
2、数e的某些性质使得它作为对数系统的底时有特殊的便利。以e为底的对数称为自然对数。用不标出底的记号ln来表示它;在理论的研究中,总是用自然对数。
数学e等于多少
数学e等于多少如下:
e是自然常数,数学中e等于值约为2.718281828。自然常数是自然对数函数的底数;有时被称为欧拉数,也是一个无限不循环小数。数学中e是无理数,在数学中是代表一个数的符号,其实还不限于数学领域。在大自然中,建构,呈现的形状,利率或者双曲线面积及微积分教科书、伯努利家族等。
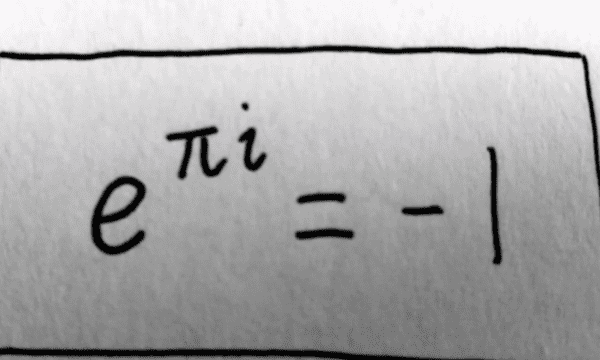
e是自然对数的底数,是一个无限不循环小数,其值是2.71828...,它是这样定义的:当n→∞时,(1+1/n)^n的极限。e,作为数学常数,是自然对数函数的底数。
有时称它为欧拉数(Euler number),以瑞士数学家欧拉命名;也有个较鲜见的名字纳皮尔常数,以纪念苏格兰数学家约翰·纳皮尔(John Napier)引进对数。它就像圆周率π和虚数单位i,e是数学中最重要的常数之一。
已知的第一次用到常数e,是莱布尼茨于1690年和1691年给惠更斯的通信,以b表示。1727年欧拉开始用e来表示这常数;而e第一次在出版物用到,是1736年欧拉的《力学》(Mechanica)。虽然以后也有研究者用字母c表示,但e较常用,终于成为标准。
e等于多少数学
数学中的e等于2.71828182。小写e,作为数学常数,是自然对数函数的底数。有时称它为欧拉数,以瑞士数学家欧拉命名。e=2.71828182……是微积分中的两个常用极限之一。
数学上e约等于多少
数学里e约等于2.71828。自然数e约等于2.71828,为数学中一个常数,是一个无限不循环小数,且为超越数。e是一个数学常数,是自然对数函数的底数,有时又称它为欧拉数,以瑞士数学课欧拉命名的。e的含义是单位时间内,持续的翻倍增长所能达到的极限值。

数学的含义概况
古代文明的数学更多地是一种实用的技术,虽然在许多方面他们的努力已经远远超过实际的需求,但这也好比各种实用技术都会发展出某种游戏性的或艺术性的维度,但实用旨趣仍然是一个基调,这和希腊之后的数学有很大区别。
比如巴比伦人会对演算结果进行“验证”,但并不在意逻辑演绎意义上的“证明”。另外,他们往往对精确解和近似解不作区分。
e约等于多少
e约等于2.71828。
e是自然对数的底数,是一个无理数,约等于2.71828。它是科学研究中非常重要的一个数学常数,在复利计算、人口增长、放射性物质衰变等问题的计算中都有广泛的应用。e的推导可以从极限的角度来理解。根据定义,e是函数f(x)=1/x在x=0处的极限。通过计算,可以得到e的无限小数表示,即e=1/(1-1/1^2)+1/(1-1/2^2)+1/(1-1/3^2)+等等。
e还与自然指数函数ex紧密相关。当函数f(x)=ex在x=0处的导数等于自身的函数值时,这个函数值就是e。通过这个性质,我们可以利用指数函数的导数公式来计算e的值。e是一个非常重要的数学常数,在自然科学、工程技术和金融等领域都有广泛的应用。

e的起源
在1690年,莱布尼茨在信中第一次提到常数e。在论文中第一次提到常数e,是约翰·纳皮尔于1618年出版的对数著作附录中的一张表。
但它没有记录这常数,只有由它为底计算出的一张自然对数列表,通常认为是由威廉·奥特雷德制作。第一次把e看为常数的是雅各·伯努利。欧拉也听说了这一常数,所以在27岁时,用发表论文的方式将e“保送”到微积分。
以上就是关于数学e等于多少,自然底数e等于多少的全部内容,以及自然底数e等于多少的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。







