二阶混合导数几何意义
二阶混合偏导数定义:
对函数先关于其中一个自变量求一次导数,再在此基础上关于另一个自变量求一次导数,即d(dy/dx1)/dx2
二阶混合导数意义如下:
1、斜线斜率变化的速度。可根据其斜率大小判断。
2、函数的凹凸性。二阶导数是比较理论的、比较抽象的一个量,它不像一阶导数那样有明显的几何意义,因为它表示的是一阶导数的变化率。在图形上,它主要表现函数的凹凸性,直观的说,函数是向上突起的,还是向下突起的。
二阶导数有何实际意义呢
二次求导的意义就是一阶导数的变化率,也就是一阶导数变化率的变化率。用法:二阶导数可以反映图象的凹凸。二阶导数大于0,图象为凹;二阶导数小于0,图象为凸;二阶导数等于0,不凹不凸。 扩展资料 结合一阶、二阶导数可以求函数的极值。当一阶导数等于零,而二阶导数大于零时,为极小值点;当一阶导数等于零,而二阶导数小于零时,为极大值点;当一阶导数、二阶导数都等于零时,为驻点。
二阶导数的几何意义
1、切线斜率变化的速度,表示的是一阶导数的变化率。
2、函数的凹凸性(例如加速度的方向总是指向轨迹曲线凹的一侧)。
二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数yˊ=fˊ(x)仍然是x的函数,则y′′=f′′(x)的导数叫做函数y=f(x)的二阶导数。在图形上,它主要表现函数的凹凸性。
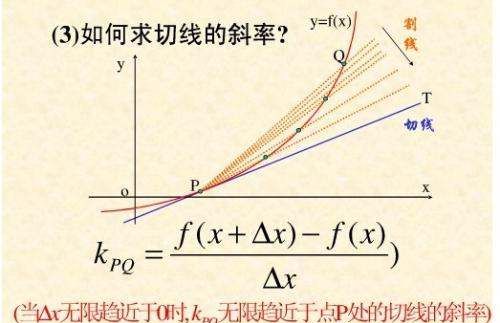
扩展资料导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。
导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。
不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
对于可导的函数f(x),x↦f'(x)也是一个函数,称作f(x)的导函数(简称导数)。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上,求导就是一个求极限的过程,导数的四则运算法则也来源于极限的四则运算法则。
反之,已知导函数也可以倒过来求原来的函数,即不定积分。微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作,它们都是微积分学中最为基础的概念。
二阶偏导数f12什么意思
f指第一未知数整体求偏导,f2指对第二未知数整体求偏导,f11是对x求完一阶偏导后的结果再对x求偏导,f22是对y求完偏导之后的结果再对y求偏导。
二阶导数是一阶导数的导数,从原理上,它表示一阶导数的变化率;从图形上看,它反映的是函数图像的凹凸性。
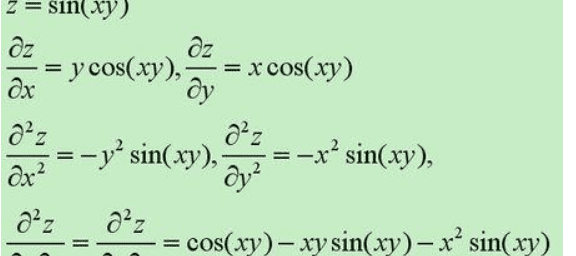
扩展资料:
二阶混合偏导数意义:
对于一个多项式函数来说,指的就是xy项的系数。
对于一般的光滑函数来说,指的是其二阶逼近中xy项的系数。
一定程度上(在二阶逼近意义上)指的是这个函数可以表示成:f(x,y) = g(x) + h(y) 这种形式的障碍。如果一个函数可以表达成这种形式那么混合偏导数一定是0。
几何上可以看成是 y方向变化率 在x方向的变化率,他同时也等于x方向的变化率在y方向的变化率。
二阶混合偏导数的几何意义是什么
一楼所言.是一阶偏导数的几何意义.
“二阶混合偏导数”,没有能够“直接看出”的“几何意义”.
当然 ,一定要,也不是不能做出来.
F〃xy(x0,y0)=(F′x(x0,y)'y(y0)
也就是,先作一个一元函数Φ(y)=F′x(x0,y),图像z=Φ(y)在(y0,Φ(y0))处的切线的斜率,就是F〃xy(x0,y0)的“几何意义”.
只能这样,它麻烦,它看不清.所以,不如干脆说,二阶混合偏导数 没有 明显的几何意义.
以上就是关于二阶混合导数几何意义,二阶导数有何实际意义呢的全部内容,以及二阶混合导数几何意义的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。