如何表示不等式的解集
不等式的解集可以在数轴上表示,每个不等式表示有两个要素,第一是起点,若是大于等于或者小于等于就在那个点上用实心点,否则用空心点,若是大于方向向右,小于方向向左。
一般用纯粹的大于号“>”、小于号“,≥,≤,≠)连接的式子叫做不等式。
什么是不等式的解集
在数轴上,自变量满足不等式的取值范围,就是不等式的解集。
不等式的解集是一个“数的集合”,是一个未知数的取值范围,特殊情况下也可能是具体的几个数。首先把每一个不等式的解集求出来,再求它们的公共部分,便得不等式组的解集。在初高中教学中,一般研究的是一元一次不等式,一元二次不等式,以及多元高次不等式组。不等式的解集一般求解的时候先将不等号看成等号来借方程,然后求出具体解之后结合不等号方向确定具体的解集。
重点:我们可以采用数轴的方法来理解,解集就是在数轴上不断的取点,所有满足这个不等式的所有点所组成的集合,就是这个不等式的解集。
一元二次不等式的解集怎么表示
表示不等式的解集有两种方法:
1、列举法:列举法也被叫做外延法,具体方法是把集合中的每个元素逐个列举,并将其全部写在大括号中,再以逗号隔开即可。
2、描述法:描述法也被叫做特征性质法或是内涵法,具体方法是根据概括原则找出确定集合元素的特征性质,并将其性质表述成一个式子或一句话的形式即可。
如何计算不等式的解集
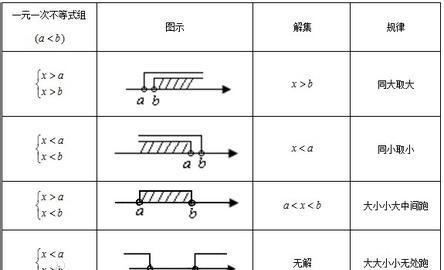
口诀有:大大取大,小小取小;大小小大,左小右大;大大小小,无解算了。用不等号(<,>,≥,≤,≠)连接的式子叫做不等式包括严格不等式、非严格不等式。
对于求出的各个不等式的解集是同向不等式的情况,其公共部分可归纳为:同大同小,分为两种:大大取大,小小取小。其中,大大取大,意即要大就取比大的那个数还要大。小小取小,意即要小就取比小的那个数还要小。
对于求出的各个不等式的解集是异向不等式的情况,其公共部分可归纳为:一大一小,也分两种:大小小大,左小右大;大大小小,无解算了。其中“大小小大,左小右大”意即大于小的,小于大的,公共部分写成左边数小,右边数大,中间为未知数,然后用“<”号连接的形式。“大大小小,无解算了”,意即大的,而又小于小的(或比大的大,比小的小),公共部分就为无解。
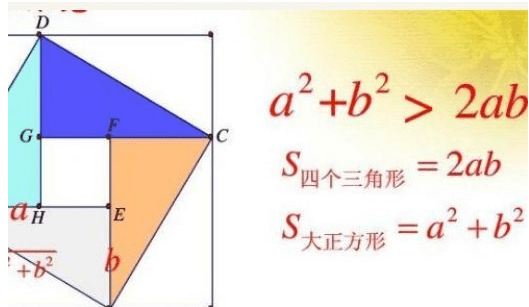
确定解集:
1、比两个值都大,就比大的还大(同大取大)。
2、比两个值都小,就比小的还小(同小取小)。
3、比大的大,比小的小,无解(大大小小取不了)。
4、比小的大,比大的小,有解在中间(小大大小取中间)。
三个或三个以上不等式组成的不等式组,可以类推。
如何计算不等式的解集
一、 绝对值定义法
对于一些简单的,一侧为常数的含不等式绝对值,直接用绝对值定义即可,
1、如|x|
2、|x| ≥ a同理可在数轴上表示出来,因此可得到解集为x≥ a或x≤ a
3、|ax +b| ≥ c型,利用绝对值性质化为不等式组−c ≤ ax + b ≤ c,再解不等式组。
二、平方法
对于不等式两边都是绝对值时,可将不等式两边同时平方。
解不等式 |x+ 3| > |x− 1|将等式两边同时平方为(x + 3)2 > (x − 1)2得到x2 + 6x + 9 > x2 − 2x + 1之后解不等式即可,解得x > −1
三、零点分段法
对于不等式中含有有两个及以上绝对值,且含有常数项时,一般使用零点分段法。例 解不等式|x + 1| + |x − 3| > 5
在数轴上可以看出,数轴可以分成x <−1,−1 ≤ x <3, x ≥ 3三个区间,由此进行分类讨论。
当x <−1时,因为x + 1 <0, x − 3 <0所以不等式化为 −x− 1 −x + 3 > 5解得x <−322.当−1 ≤x <3时, 因为x + 1 > 0,x− 3 <0所以不等式化为x + 1 − x + 3 > 5无解。
当 x ≥ 3时 因为x + 1 > 0 ,x − 3 > 0所以不等式化为x + 1 + x− 3 > 5解得x >72综上所述,不等式的解为x <−32或x >72。

扩展资料
1、实数的绝对值的概念
(1)|a|的几何意义
|a|表示数轴上实数a对应的点与原点之间的距离.
(2)两个重要性质
①(ⅰ)|ab|=|a||b|
②|a|<|b|⇔a2
(3)|x-a|的几何意义:数轴上实数x对应的点与实数a对应的点之间的距离,或数轴上表示x-a的点到原点的距离.
(4)|x+a|的几何意义:数轴上实数x对应的点与实数-a对应的点之间的距离,或数轴上表示x+a的点到原点的距离。
2、绝对值不等式定理
(1)定理:对任意实数a和b,有|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立.
(2)定理的另一种形式:对任意实数a和b,有|a-b|≤|a|+|b|,当且仅当ab≤0时,等号成立.
绝对值不等式定理的完整形式:|a|-|b|≤|a±b|≤|a|+|b|.
其中,(1)|a+b|=|a|-|b|成立的条件是ab≤0,且|a|≥|b|;
(2)|a+b|=|a|+|b|成立的条件是ab≥0;
(3)|a-b|=|a|-|b|成立的条件是ab≥0,且|a|≥|b|;
(4)|a-b|=|a|+|b|成立的条件是ab≤0.
以上就是关于什么是不等式的解集,如何表示不等式的解集的全部内容,以及如何表示不等式的解集的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。