多项式的定义 什么是常数项
1、在数学中,由若干个单项式相加组成的代数式叫做多项式(若有减法:减一个数等于加上它的相反数)。
多项式中的每个单项式叫做多项式的项,这些单项式中的最高项次数,就是这个多项式的次数。
其中多项式中不含字母的项叫做常数项。
什么是多项式什么是多项式中的常数式什么是多项式的几次几项式 回答要简洁易懂
多项式:几个单项式的和叫多项式,例:2a+3b,3x³y-8z+1
单项式:只含有数字与字母的积或正整数次幂组成的代数式叫单项式,单独的一个数或一个字母也叫单项式;例:3x³y、0;
常数项:不含有未知数的的项就是常数项
几次几项式 是针对多项式而言;多项式的项数是单项式的个数,次数是所有单项式里面次数最高的项的次数,例:2a+3b是一次二项式,3x³y-8z+1是四次三项式.
什么是一个多项式的常数项
常数项指的是多项式中,每个单项式上不含字母的项。例如在多项式6X-2X+7中,6X、-2X和7是它的项,其中7是常数项。
常数是指固定不变的数值。就是除了字母以外的任何数,包括正负整数和正负小数、分数、0和无理数(如π)。如圆的周长和直径的比π﹑铁的膨胀系数0.000012等。
常数具有一定含义的名称,用于代替数字或字符串,其值从不改变。数学上常用大写的"C"来表示某一个常数。一个数学常数,是指一个数值不变的常量,与之相反的是变量。跟大多数物理常数不一样的地方是,数学常数的定义是独立于所有物理测量的。
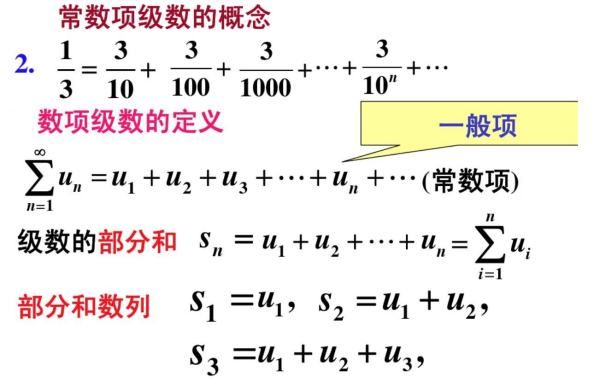
扩展资料多项式是一类简单的初等函数,而且任给两组数:b1,b2,…,bn+1和各不相同的 с1,с2,…,сn+1,总有唯一的次数不超过n的多项式ƒ(x)满足ƒ(сi)=bi,i=1,2,…,n+1。因此在实际应用中常常取多项式作为插值函数。作为插值函数的多项式,称为插值多项式。插值多项式在计算数学插值中最常用。
在实际问题中,往往通过实验或观测得出表示某种规律的数量关系y=F(x),通常只给出了F(x)在某些点xi上的函数值yi=F(xi),j=1,2,…,n+1。即使有时给出了函数F(x)的解析表达式,倘若较为复杂,也不便于计算。因此,需要根据给定点 xi 上的函数值F(xi),求出一个既能反映F(x)的特性,又便于计算的简单函数ƒ(x)来近似地代替F(x),此时ƒ(x)称为F(x)的插值函数;x1,x2,…,xn+1,称为插值节点。求插值函数的方法,称为插值法。
多项式的常数项是指什么
常数项是多项式中不含字母的项。
多项式中不含有字母的项叫常数项,多项式中次数最高的那一个单项式的系数,叫做最高次项的系数,如 5xy^3+8xy+9 中,9为常数项,最高次项的系数为5。
已知多项式是由四个单项式相加构成,且第三项次数最高为四次,即可得到此多项式为四次四项式,找出最高项系数及常数项即可。
扩展资料:
注意事项:
常数是具有一定含义的名称,用于代替数字或字符串,其值从不改变。数学上常用大写的"C"来表示某一个常数。一个数学常数,是指一个数值不变的常量,与之相反的是变量。
跟大多数物理常数不一样的地方是,数学常数的定义是独立于所有物理测量的。多项式中,每个单项式上不含字母的项叫常数项。
什么是多项式的常数项
多项式中,每个单项式上不含字母的项,包括正负整数和正负小数、分数、0和无理数(如π)。数学上常用大写的"C"来表示。
1.多项式的定义
首先,我们需要了解多项式的定义。多项式是由一系列有限项组成的代数表达式,每一项包含一个系数和一个变量的幂次。常数项是其中的一种特殊情况。

2.多项式的一般形式
多项式的一般形式可以表示为:P(x)=aₙxⁿ+aₙ₋₁xⁿ⁻¹+...+a₁x+a₀。其中,aₙ,aₙ₋₁,...,a₁,a₀是多项式的系数,x是变量,n是多项式的次数。
3.常数项的定义
在多项式中,当某一项的指数为0时,即变量的幂次为0,这一项就成为常数项。常数项没有变量,只包含一个系数,也就是一个常数。
4.常数项的示例
举个例子,考虑一个多项式P(x)=3x²+2x-7。在这个多项式中,常数项是-7。因为当x的幂次为0时,对应的系数是-7,没有x变量存在。
5.常数项的性质
常数项在整个多项式的运算中起着重要的作用。它可以影响多项式的值和性质。例如,在多项式的求和、差、积以及除法运算中,常数项的系数会直接影响结果的计算和性质的变化。
6.常数项的意义
常数项在多项式中的意义取决于具体的问题和背景。在一些应用中,常数项可能代表某种常数或初始值,反映了一种起始状态。它可以用于描述问题的特定条件或约束。

总结起来,多项式中的常数项是指没有变量的项,其系数是一个常数。常数项在多项式的定义、运算和应用中起着重要的作用,它可以影响多项式的值和性质。理解和分析常数项的意义对于理解多项式的整体结构和性质是非常重要的。
以上就是关于多项式的定义 什么是常数项的全部内容,以及多项式的定义 什么是常数项的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。