两直线位置关系公式
两直线位置关系公式的为:已知直线l1:y=k1x+b1,l2:y=k2x+b2。
l1//l2则k1=k2,b1≠b2,l1⊥l2,k1k2=-1。
若两条直线平行,则两直线距离公式为:设l1:Ax+By+C1=0,l2:Ax+By+C2=0,d=|C1-C2|/√(A?+B?)。
如何用方程表示两条直线的位置关系图
假设已知的两条相交直线的方程分别为 A x + B y + C = 0 和 D x + E y + F = 0。
构造以下一条直线:
A x + B y + C + k (D x + E y + F) = 0
则这条直线一定经过已知两条直线的交点(因为该交点的座标必定同时满足前两条直线的方程,所以,交点座标也必然会满足这构造出的第三条直线的方程——这就说明这第三条直线必过已知交点)。当 k = 0 时,这个方程其实就表示了第一条已知直线。注意,无论 k 取何值,这个方程都无法代表第二条已知直线。事实上,这个方程(可整理成标准形式如 (A + k D) x + (B + k E) y + C + k F = 0)可以代表经过前述交点的除第二条已知直线外的所有直线。
当然,也可构造这么一条直线 k (A x + B y + C) + D x + E y + F = 0 (可写成标准式 (k A + D) x + (k B + E) y + k C + F = 0),它可以表示经过交点的——除第一条已知直线以外——的所有直线。
判断直线ab与直线cd的位置关系
两直线的位置关系可以分为两类:
①同一平面中:
平行,相交,重合
②两个平面中:
异面直线
二、两直线平行和垂直的判定
两直线平行和垂直的判定分为两类,一种是点斜式进行判定,一种是一般式进行判定.
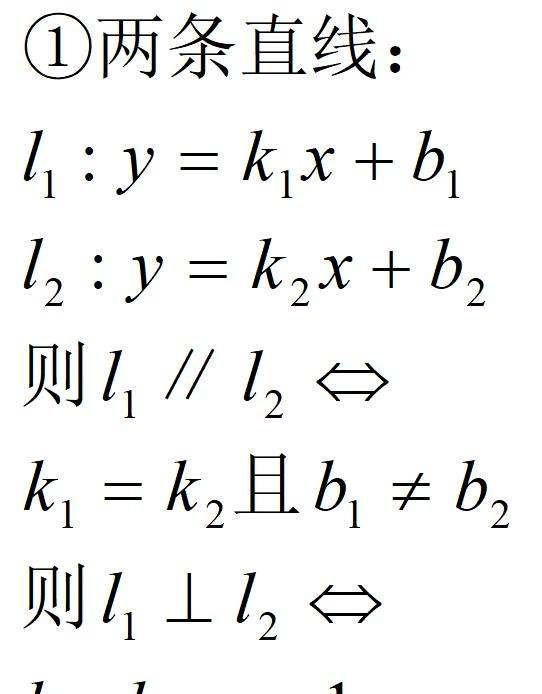
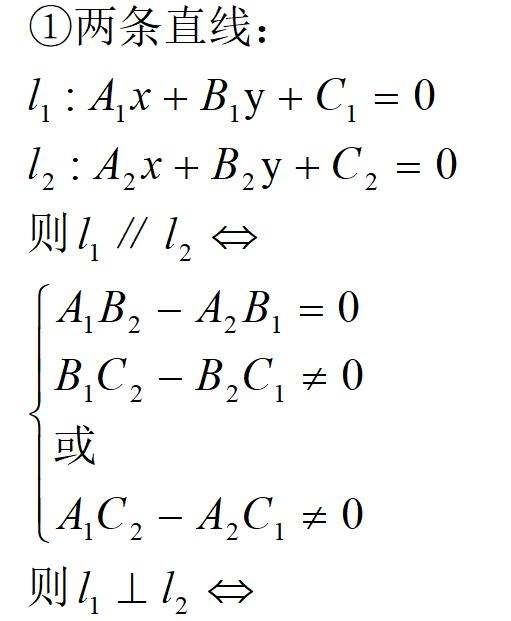
解析:
①平行:
②垂直:
Bx -Ay+m=0
三、解题思路
(1) 两直线平行:
两直线的斜率相等且在坐标轴上的截距不等,或者两直线的斜率都不存在且两直线在x轴上的截距不相等.
(2) 两直线垂直:
两直线的斜率之积等于-1,或者一条直线的斜率为0且另一条直线斜率不存在.
有关直线方程和两直线位置关系 的公式是什么
ax+by+c=0
k=-a/b
平行 a1:a2=b1:b2不等于c1:c2 或k1=k2(若斜率存在)
重合 a1:a2=b1:b2=c1:c2
方程
一般式 ax+by+c=0
斜截式(斜率存在) y=kx+b
点斜式(斜率存在) y-y1=(y1-y2)/(x1-x2)*(x-x1)
截距式(截距均不为0)x/a+y/b=1
两条直线的位置关系教学视频
直线L1:A1x+B1y+C1=0
直线L2:A2x+B2y+C2=0
当A1=A2,B1=B2,C1=C2时,两直线重合。
当A1=A2,B1=B2,C1≠C2时,两直线平行。
当A1*B2+A2*B1=0时,两直线垂直。
若A1,A2,B1,B2,C1,C2以上关系都不满足,那就是不垂直的相交了。
以上就是关于两直线位置关系公式,如何用方程表示两条直线的位置关系图的全部内容,以及两直线位置关系公式的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。