回归方程拟合效果公式
回归方程拟合效果公式是“R^2=∑(y预测-y)^2/==∑(y实际-y)^2”或者“R^2=1-(Q/∑y^2)^(1/2)”,其中y是平均数。
回归方程是根据样本资料并通过回归分析所得到的反映一个变量(因变量)对另一个或一组变量(自变量)的回归关系的数学表达式,回归直线方程用得比较多,可以用最小二乘法求回归直线方程中的a,b,从而得到回归直线方程。
线性回归拟合方程公式excel
线性回归都可以通过最小二乘法求出其方程,可以计算出对于y=bx+a的直线。
拟合是推求一个函数表达式y=f(x)来描述y和x之间的关系,一般用最小二乘法原理来计算。用直线来拟合时,可以叫一次曲线拟合,虽然有点别扭;用二次函数来拟合时,可以叫抛物线拟合或二次曲线拟合,但不能说线性回归。
用直线(y=ax+b)拟合时,得到的方程和一元线性回归分析得到的方程是一样的,但是拟合时可以人为指定函数参数形式,如b=0,而线性回归分析目的则侧重于描述y和x线性相关的程度,通常会同时计算相关系数、F检验值等统计参数。

求解方法
线性回归模型经常用最小二乘逼近来拟合,但他们也可能用别的方法来拟合,比如用最小化“拟合缺陷”在一些其他规范里(比如最小绝对误差回归),或者在回归中最小化最小二乘损失函数的乘法。相反,最小二乘逼近可以用来拟合那些非线性的模型。因此,尽管最小二乘法和线性模型是紧密相连的,但他们是不能划等号的。
以上内容参考:
拟合度计算公式excel
拟合度r2计算公式:R2=ESS/TSS=1-RSS/TSS,拟合度检验是对已制作好的预测模型进行检验,比较它们的预测结果与实际发生情况的吻合程度。

扩展资料:
R2衡量回归方程整体的拟合度,是表达因变量与所有自变量之间的总体关系。R²等于回归平方和在总平方和中所占的比率,即回归方程所能解释的因变量变异性的百分比(在MATLAB中,R²=1-"回归平方和在总平方和中所占的比率")。
实际值与平均值的总误差中,回归误差与剩余误差是此消彼长的关系。因而回归误差从正面测定线性模型的拟合优度,剩余误差则从反面来判定线性模型的拟合优度。

统计上定义剩余误差除以自由度n–2所得之商的平方根为估计标准误。为回归模型拟合优度的判断和评价指标,估计标准误显然不如判定系数R²。R²是无量纲系数,有确定的取值范围 (0—1),便于对不同资料回归模型拟合优度进行比较。
而估计标准误差是有计量单位的,又没有确定的取值范围,不便于对不同资料回归模型拟合优度进行比较。
线性回归方程的公式是什么意思
线性回归方程的公式如下图所示:
先求x,y的平均值X,Y
再用公式代入求解:b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)
后把x,y的平均数X,Y代入a=Y-bX
求出a并代入总的公式y=bx+a得到线性回归方程。
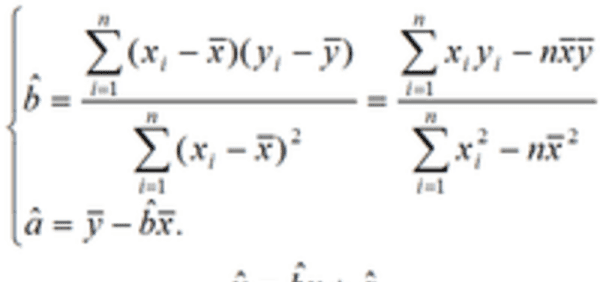
扩展资料
线性回归方程是利用数理统计中的回归分析,来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法之一。线性回归也是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。按自变量个数可分为一元线性回归分析方程和多元线性回归分析方程。
在统计学中,线性回归方程是利用最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。(这反过来又应当由多个相关的因变量预测的多元线性回归区别,而不是一个单一的标量变量。)
参考资料
以上就是关于回归方程拟合效果公式,线性回归拟合方程公式excel的全部内容,以及回归方程拟合效果公式的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。