梯形的体积怎么求
梯形的体积=(上底+下底)×高÷2×总长度。梯形是只有一组对边平行的四边形。平行的两边叫做梯形的底边:较长的一条底边叫下底,较短的一条底边叫上底;另外两边叫腰;夹在两底之间的垂线段叫梯形的高。
体积,几何学专业术语。当物体占据的空间是三维空间时,所占空间的大小叫做该物体的体积。体积的国际单位制是立方米。一维空间物件(如线)及二维空间物件(如正方形)都是零体积的。
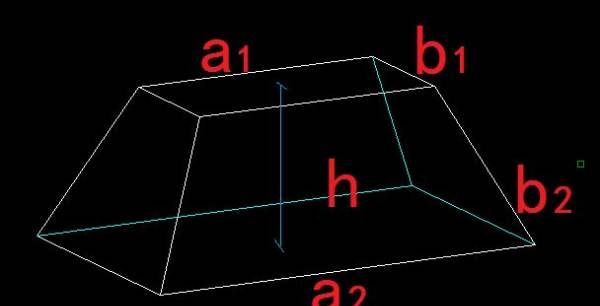
梯形的体积计算公式图
第一种:梯形的体积=(上底+下底)×高÷2×总长度
第二种:把四棱台延长成椎上截面面积为s,下截面r,台高为h,那么体积=1/3(r-s)*h.
若是正梯形物体则为
V=〔S1+S2+开根号(S1*S2)〕/3*H
注:V:体积;S1:上表面积;S2:下表面积;H:高。
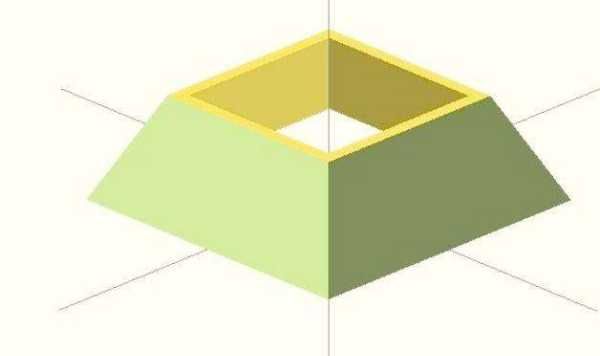
1、定义
上、下面平行且为长方形(特殊情况有两个相对的面是正方形,即四棱台),四个侧面都是梯形由此围成的立体图形叫梯形体.
2、PS画出梯形体的方法是:
(1)新建背景文件,创建新图层,用“进行选框工具”画矩形,填充灰色;
(2)“编辑--变换--透视”变换成梯形,复制,移动,用“多边形套索工具”连接其他各点,制作其他侧面,变成梯形体;
(3)根据光线情况,在不同侧面拉黑白渐变,制作效果,完成。
梯形体积怎么算
梯形体的体积计算公式:
V=[S1 + √(S1*S2) + S2] * H/3
V是总体积,S1是上面积,S2是下面积,H是高。
梯形的面积计算公式:
S=1/2 * (a+b) * H
S是总面积,a上底,b是下底,H是高。
扩展资料:
1、立方和公式
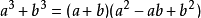
2、立方差公式
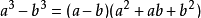
3、三项立方和公式
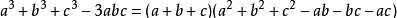
4、推导过程:
a、立方和:
a³+b³=a³+a²b-a²b+b³=a²(a+b)-b(a²-b²)=a²(a+b)-b(a+b)(a-b)=(a+b)[a²-b(a-b)]=(a+b)(a²-ab+b²)
b、立方差:
a3-b3=a3-b3+a2b-a2b=a2(a-b)+b(a2-b2)=a2(a-b)+b(a+b)(a-b)=[a2+b(a+b)](a-b)=(a-b)(a2+ab+b2)
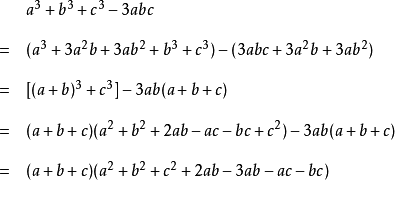
c、完全立方公式
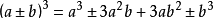
分解步骤如下
(a+b)3=(a+b)(a+b)(a+b) = (a2+2ab+b2)(a+b)=a3+3a2b + 3ab2+ b3
解题时常用它的变形:
(a+b)3= a3+ b3+ 3ab(a+b)和a3+ b3= (a+b)3- 3ab(a+b)
(a-b)³=(a-b)(a-b)(a-b)=(a²-2ab+b²)(a-b)=a³-3a²b+3ab²-b³
立方和累加
正整数范围中
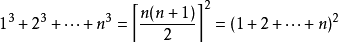
注:可用数学归纳法证明
梯形的体积怎么算
梯形立方体积计算公式:梯形的体积=(上底+下底)×高÷2×总长度。
梯形的体积=(上底+下底)×高÷2×总长度,体积,或称容量、容积,几何学专业术语,是物件占有多少空间的量。体积的国际单位制是立方米。件固体物件的体积是一个数值用以形容该物件在三维空间所占有的空间。
梯形是指一组对边平行而另一组对边不平行的四边形。平行的两边叫做梯形的底边,长的一条底边叫下底,短的一条底边叫上底。不平行的两边叫腰。
夹在两底之间的垂线段叫梯形的高。一腰垂直于底的梯形叫直角梯形。两腰相等的梯形叫等腰梯形。等腰梯形是一种特殊的梯形,其判定方法与等腰三角形判定方法类似。
学习数学重要性:
1、数学与我们生活息息相关。要说学数学的真正效果,它不是体现在应试教育上,而是将来自身的思维上。

2、数学的重要性不言而喻。数学是一切科学的基础,是培养逻辑思维重要渠道,可以说我们人类的每一次重大进步都有数学这门学科在做强有力的支撑。
3、生活中的数学知识运用无处不在。从日常生活中柴米油盐的费用的计算,到天文地理、质量控制、农业经济、航天事业都存在着运用数学的影子。
以上就是关于梯形的体积怎么,梯形的体积计算公式图的全部内容,以及梯形的体积怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。