3ax的导数怎么求
把x的次数化为0,即3ax的导数为3a。导数是微积分学中重要的基础概念,是函数的局部性质。
当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数。不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。
y=x的x次方的导数
(a^3x)'
=a^3x*lna*(3x)'
=3a^3x*lna
y等于a的3x次方的导数
y=a^x的导数:a^xlna。
y=a^x
lny=ln(a^x)=xlna
两边对x求导1/y*dy/dx=lna*1dy/dx=lna*y
dy/dx=a^xlna
扩展资料:
由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。基本的求导法则如下:
1、求导的线性:对函数的线性组合求导,等于先对其中每个部分求导后再取线性组合(即①式)。
2、两个函数的乘积的导函数:一导乘二+一乘二导(即②式)。
3、两个函数的商的导函数也是一个分式:(子导乘母-子乘母导)除以母平方(即③式)。
4、如果有复合函数,则用链式法则求导。
3x的导数怎么算
in3次方x的导数是(ln3)(3^x)cos(3^x);
若y=sin³x
则y`=3sin²x(sinx)`=3sin²xcosx
若y=sin(3^x)
则y`=cos(3^x)(3^x)`=cos(3^x)3^xln3=(ln3)(3^x)cos(3^x)
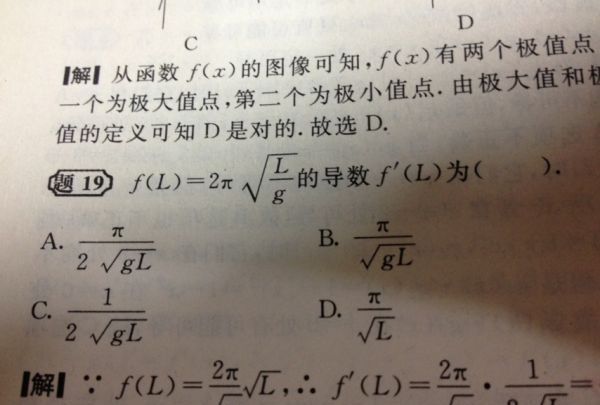
发展
17世纪生产力的发展推动了自然科学和技术的发展,在前人创造性研究的基础上,大数学家牛顿、莱布尼茨等从不同的角度开始系统地研究微积分。牛顿的微积分理论被称为“流数术”,他称变量为流量,称变量的变化率为流数,相当于我们所说的导数。
牛顿的有关“流数术”的主要著作是《求曲边形面积》、《运用无穷多项方程的计算法》和《流数术和无穷级数》,流数理论的实质概括为:他的重点在于一个变量的函数而不在于多变量的方程;在于自变量的变化与函数的变化的比的构成;最在于决定这个比当变化趋于零时的极限。
基本函数的导数公式
函数的导数是函数在某个点处的变化率,它通常用于描述函数的趋势和特征。求函数的导数是数学中的一个重要概念,以下是求解函数导数的常用方法:
基本法则法:基本法则法是求解函数导数的一种常用方法。它通过应用导数的基本概念和基本法则,如常数因子法则、乘积法则、商法则等,直接求解函数在某一点的导数。
差商法:差商法适用于求解形如y=f(x)的函数在某一点的导数。它通过将函数在两个不同点处的函数值之差与这两个点之间的直线的斜率相除,得到函数在该点的导数。
对数法:对数法适用于求解形如y=f(x)的函数在某一点的导数。它通过将函数在两个不同点处的函数值之差对这两个点之间的对数进行积分,得到函数在该点的导数。
幂法:幂法适用于求解形如y=a^x的函数在某一点的导数。它通过将函数在两个不同点处的函数值之差对这两个点之间的幂次进行积分,得到函数在该点的导数。
以上是求解函数导数的常用方法,具体选择哪种方法取决于函数的性质和问题的要求。
以上就是关于3ax的导数怎么,y=x的x次方的导数的全部内容,以及3ax的导数怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。