反比例函数渐近线怎么求
y=正负(√2)x。反比例指的是两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,那么它们就叫做成反比例的量,它们的关系叫做反比例关系。
渐近线是指曲线上一点M沿曲线无限远离原点或无限接近间断点时,如果M到一条直线的距离无限趋近于零,那么这条直线称为这条曲线的渐近线。
反比例函数求渐近线
用:
k=lim (x->∞)【6x/(32-5x)】/x
=lim (x->∞)【6/(32-5x)】
=0
所以
不存在斜渐近线
水平渐近线
y=-6/5
双曲线的渐近线方程公式是什么
双曲线渐近线方程公式:方程:y=±(b/a)x(当焦点在x轴上),y=±(a/b)x (焦点在y轴上)或令双曲线标准方程 x^2/a^2-y^2/b^2 =1中的1为零即得渐近线方程。
双曲线x^2/a^2-y^2/b^2 =1的简单几何性质:
1、范围:|x|≥a,y∈R。
2、对称性:双曲线的对称性与椭圆完全相同,关于x轴、y轴及原点中心对称。
3、顶点:两个顶点A1(-a,0),A2(a,0),两顶点间的线段为实轴,长为2a,虚轴长为2b,且c^2=a^2+b^2,与椭圆不同。
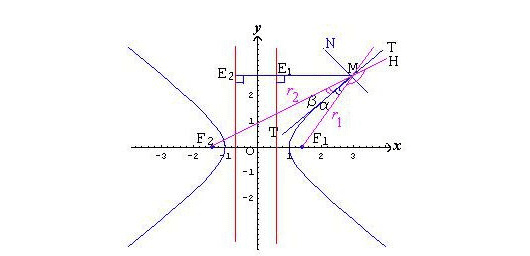
渐近线特点:
无限接近,但不可以相交。分为垂直渐近线、水平渐近线和斜渐近线,当曲线上一点M沿曲线无限远离原点时,如果M到一条直线的距离无限趋近于零,那么这条直线称为这条曲线的渐近线。
需要注意的是:并不是所有的曲线都有渐近线,渐近线反映了某些曲线在无限延伸时的变化情况。根据渐近线的位置,可将渐近线分为三类:水平渐近线、垂直渐近线、斜渐近线。
y=k/x(k≠0)是反比例函数,其图象关于原点对称,x=0,y=0为其渐近线方程。
当焦点在x轴上时 双曲线渐近线的方程是y=[+(-)b/a]x。
当焦点在y轴上时 双曲线渐近线的方程是y=[+(-)a/b]x。
反比例函数的渐近线是什么
1)垂直渐近线:解得使分母为0的点x0,lim(x→x0)f(x)=无穷,x=x0是垂直渐近线,比如y=3x/(x+1),lim(x→-1)[3x/(x+1)]=无穷,x=-1是垂直渐近线.2)水平渐近线:lim(x→无穷)f(x)=b,y=b是水平渐近线.比如lim(x→无穷)[...
反比例函数的渐进线
对于过原点的反比例函数。坐标系的两个数轴就是它的渐近线。
以上就是关于反比例函数求渐近线,反比例函数渐近线怎么的全部内容,以及反比例函数渐近线怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。