椎体的体积怎么求
棱锥体积公式:V=1/3Sh,公式中s为底面积,h为四棱锥的高。锥体是指包括圆锥、棱锥等在内的空间立体图形,由圆的或其它封闭平面基底以及由此基底边界上各点连向一公共顶点的线段所形成的面所限定。
立体图形(solidfigure)是各部分不在同一平面内的几何图形,由一个或多个面围成的可以存在于现实生活中的三维图形。点动成线,线动成面,面动成体。即由面围成体,看一个长方体,正方体等的规则立体图形最多看到立体图形实物的三个面。
锥体的体积怎么算?
锥体的体积公式是:
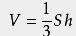
S是底面积,h是高。
椎体
1、含义:
椎体是指包括圆锥、棱锥等在内的空间立体图形,由圆的或其它封闭平面基底以及由此基底边界上各点连向一公共顶点的线段所形成的面所限定。
2、概念:
圆锥的高:圆锥的顶点到圆锥的底面圆心之间的距离叫做圆锥的高;
圆锥母线:圆锥的侧面展开形成的扇形的半径、底面圆周上任意一点到顶点的距离。
圆锥的侧面积:将圆锥的侧面沿母线展开,是一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长. 圆锥的侧面积就是弧长为圆锥底面的周长×母线/2;没展开时是一个曲面。
圆锥有一个底面、一个侧面、一个顶点、一条高、无数条母线,且底面展开图为一圆形侧面展开图是扇形。
圆锥侧面展开是一个扇形,已知扇形面积为二分之一rl。所以圆锥侧面积为二分之一母线长×弧长(即底面周长)。另 外,母线长等于底面圆直径的圆锥,展开的 扇形就是半圆。所有圆锥展开的扇形角度等于(底面直径÷母线)×180度。
体积:
一个圆锥所占空间的大小,叫做这个圆锥的体积.
一个圆锥的体积等于与它等底等高的圆柱的体积的1/3
根据 圆柱体积公式V=Sh(V=πr2×h),得出圆锥体积公式:V=1/3Sh
S是圆锥的底面积,h是圆锥的高,r是圆锥的底面半径。
得出圆锥公式V=1/3Sh
截锥体的体积公式是什么
设两底为矩形,a1,b1,a,b分别为上下底边长,h为高。截头方锥体体积公式为:V=h/6[ab+(a+a1)(b+b1)+a1b1]。
截锥体是一种与锥体有关的多面体,指由平面截锥体而得的另一个锥体。锥体被不过顶点且与锥体母线都相交的平面所截,留下的在截面和底面间的锥体部分。
截头方椎体性质:两个底面是相似多边形。各侧棱的延长线交于一点。侧面都是梯形。对角面是梯形。与棱台底面平行的截面是和底面相似的多边形。
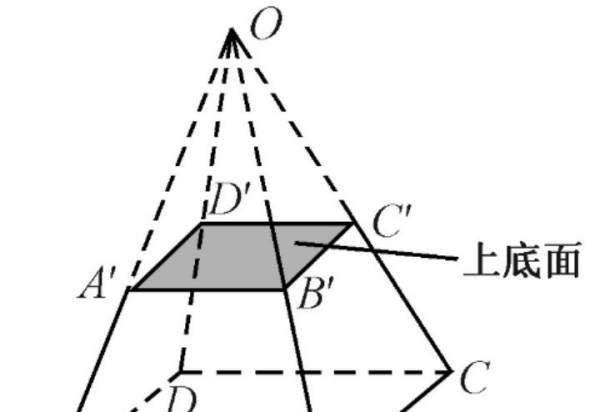
扩展资料椎体通用体积公式:
1、椎体常规公式:
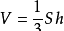
其中S是底面积,h是高。
2、圆锥体的圆锥体体积=
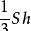
其中S是底面积,h是高。
3、三棱锥:三棱锥是立体空间中最普通最基本的图形,正如三角形之于二维空间。
已知空间内三角形三顶点坐标A(
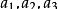
),B(
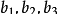
),C(
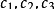
),O为原点,则三棱锥O-ABC的体积为:
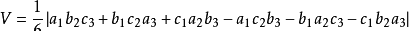
。
参考资料:
规则物体的体积公式
立方体,柱体,棱柱体体积:V=Sh,即体积等于底面积乘高
锥体的体积:V=1/3Sh
球体体积=4/3×π×r³
没有通用的,只能分开计算
椎体保温的体积计算公式
锥体积计算公式:V=1/3Sh,公式中s为底面积,h为高。
锥体的体积公式=底面积×高×1/3,如圆锥即为:V=1/3πR²h(R为底面圆的半径,h为高)。体积公式用于计算体积的公式,体积公式也值不同体积单位之间进行换算所用的公式。
(1)一个圆锥所占空间的大小是圆锥的体积;
(2)一个圆锥的体积等于与它等底等高的圆柱的体积的1/3;
(3)根据圆柱体积公式:V=Sh(V=πR²h);
(4)得出圆锥体积公式:V=1/3Sh,S是圆锥的底面积,h是圆锥的高,r是圆锥的底面半径;
(5)得出圆锥公式:V=1/3Sh。

扩展资料
锥体是指包括圆锥、棱锥等在内的空间立体图形,由圆的或其它封闭平面基底以及由此基底边界上各点连向一公共顶点的线段所形成的面所限定。注意体积公式是用于计算体积的公式,即计算各种几何体(比如:圆柱、棱柱、锥体、台体、球体、椭球体等)体积的数学算式。
基本体积单位和换算:公制单位
公制体积单位包含:立方米(m³)、立方分米(dm³)、立方厘米(cm³)、立方毫米(mm³);升(l)、毫升(ml)等。其换算关系为:
(1)1m³=10³dm³=10⁶cm³=10⁹mm³;
(2)1l=1dm³
(3)1ml=1cm³

在棱柱状态下,底面与顶面a=c,b=d,则体积公式简化后为v=a.b.h在正棱锥状态下,顶面面积为0,并且是c=0,d=0.则体积公式简化为v=1/2a.b.h-1/6a.b.h=1/3a.b.h在非标准状态下棱台体积如顶面为只有长没有宽状态下的刃型体积(如横放的三棱柱)。
正棱台体积推导;顶面c=a,d=0v=1/2a.b.h(用三棱柱立式来算也是该结果)像这种非标准状态恰恰是现有公式根本无法计算的(只要不立起来算)。
以上就是关于椎体的体积怎么,锥体的体积怎么算?的全部内容,以及椎体的体积怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。