采样定理对信号的带宽要求是什么
采样定理要求采样频率必须是信号的带宽的2倍以上。
采样定理是在数字信号处理领域中,连续时间信号(通常称为“模拟信号”)和离散时间信号(通常称为“数字信号”)之间的基本桥梁。该定理说明采样频率与信号频谱之间的关系,是连续信号离散化的基本依据,为采样率建立了一个足够的条件,该采样率允许离散采样序列从有限带宽的连续时间信号中捕获所有信息。
在进行模拟/数字信号的转换过程中,当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax),采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的2.56~4倍。
频域采样定理的内容
在数字信号处理领域,采样定理是连续时间信号(模拟信号)与离散时间信号(数字信号)之间的基本桥梁。采样定理说明采样频率与信号频谱之间的关系,是连续信号离散化的基本依据。

定理: A/D转换器中,奈奎斯特定理规定采样速率必须至少是模拟信号带宽最大值的两倍,以便完全恢复信号。
适用条件: 定理仅适用于具有傅里叶变换的一类数学函数,即频率在有限区域以外为零。
混叠: 如果不能满足采样定理,采样后信号的频率就会重叠,即采样频率一半的频率成分将被重建成低于采样频率一半的信号,这种频率的重叠导致的失真称为混叠。
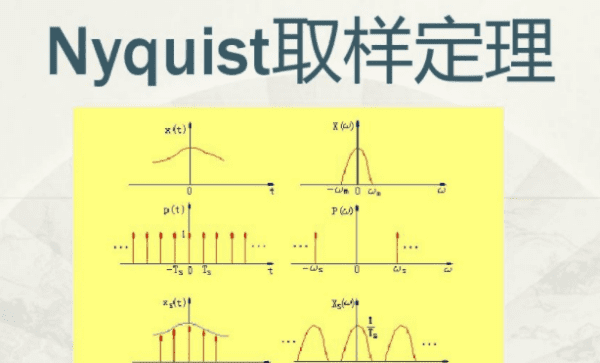
采样(信号离散化): 采样器由电子开关组成,开关每隔Ts秒短暂闭合一次。连通连续信号,实现一次采样。
采样频率为什么不能等于二倍
根据采样定理,采样频率大于等于工作频率的二倍,才能恢复出实际波形。
以正弦波为例,要完整恢复,必须正负半周都采样到,不然是恢复出的波形就变样了,所以要求采样频率大于等于二倍带宽。
采样频率必须大于被采样信号带宽的两倍,另外一种等同的说法是奈奎斯特定律必须大于被采样信号的带宽。
如果信号的带宽是100Hz,那么为了避免混叠现象采样频率必须大于200Hz。换句话说就是采样频率必须至少是信号中最大频率分量频率的两倍,否则就不能从信号采样中恢复原始信号。
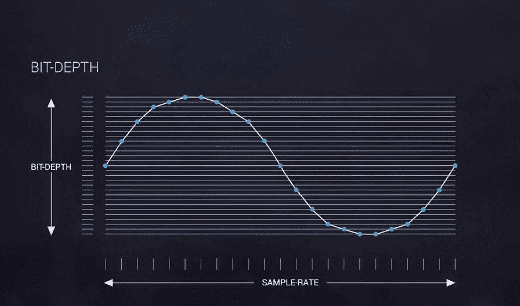
扩展资料:
在信号处理和信息理论的相关领域中,通过研究信号在经过一段距离后如何衰减以及一个给定信号能加载多少数据后得到了一个著名的公式,叫做香农(Shannon)定理。
它以比特每秒(bps)的形式给出一个链路速度的上限,表示为链路信噪比的一个函数,链路信噪比用分贝(dB)衡量。因此我们可以用香农定理来检测电话线的数据速率。
香农定理由如下的公式给出: C=Blog2(1+S/N) 其中C是可得到的链路速度,B是链路的带宽,S是平均信号功率,N是平均噪声功率,信噪比(S/N)通常用分贝(dB)表示,分贝数=10×log10(S/N)。
采样定理对信号的带宽要求是什么
采样定理要求采样频率必须是信号的带宽的2倍以上。
采样定理是在数字信号处理领域中,连续时间信号(通常称为“模拟信号”)和离散时间信号(通常称为“数字信号”)之间的基本桥梁。该定理说明采样频率与信号频谱之间的关系,是连续信号离散化的基本依据,为采样率建立了一个足够的条件,该采样率允许离散采样序列从有限带宽的连续时间信号中捕获所有信息。
在进行模拟/数字信号的转换过程中,当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax),采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的2.56~4倍。
采样定理要求采样频率大于信号最高频率的1.56倍
采样定理,也称为Nyquist定理,指出如果一个连续时间信号的频谱没有超过一定的频率,称为Nyquist频率,那么至少需要以该频率的两倍进行采样才能准确地重建出原始信号。
这里的“最大频率”通常是指信号的最高频率分量,即信号的带宽。因此,“采样频率是大于最大频率的两倍”和“采样频率是大于带宽的两倍”这两种表述实际上是等价的。
换句话说,如果一个信号的带宽为B Hz,那么采样频率应该至少为2B Hz。这是因为带宽通常被定义为能够包含信号所有频率分量的最低频率范围。因此,对于一个具有B Hz带宽的信号,至少需要2B Hz的采样频率才能准确地重建该信号。
因此,采样定理中的采样频率应该是大于或等于最大频率(即带宽)的两倍。
以上就是关于频域采样定理的内容,采样定理对信号的带宽要是什么的全部内容,以及采样定理对信号的带宽要求是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。




