解析几何弦长公式
弦长公式:指在这里指直线与圆锥曲线相交所得弦长d的公式,并且直线与圆锥曲线的位置关系是平面解析几何的重要内容之一,也是高考的热点,解析几何弦长公式为:弦长=│x1-x2│√(k^2+1)=│y1-y2│√[(1/k^2)+1],其中k为直线斜率,(x1,y1),(x2,y2)为直线与曲线的两交点。
弦长公式怎么推导出来的
弦长公式的推导过程是:设直线方程:y=kx+b与曲线C交于点A(x1,y1)及B(x2,y2),然后将其列为方程组,得出AB的绝对值=根号下x1-x2括起来的平方加上y1-y2括起来的平方,最后替换得出√(1+k²)|x1-x2|。
其中k是一个常数,A和B都是具体的点数。
弦长的含义:
弦长为连接圆上任意两点的线段的长度。弦长公式,在这里指直线与圆锥曲线相交所得弦长的公式,都是数学中进行计算需要记住的,对于后面知识的学习来说,这个公式是最基础的。
直线与圆锥曲线的位置关系也是平面解析几何的重要内容之一,主要就是考查学生关这方面掌握如何,数学也是很有逻辑性的,公式也是一一推下来的。
在数学中的运用:
弦长公式的推导也是数学中较为简单的一种推导过程,如果弄清楚公式的来龙去脉,可以加深对公式的理解,方便后面做题对于公式的应用。实用性也是很强的,可以帮助更好的解题,有了明确的思路,可以很好的节约解题的时间爱你,提高做题的效率。
高中数学弦长公式推导过程
|AB|=[根号下(1+k^2)]乘以|x2-x1|=[根号下(1+1/k^2)]乘以|y2-y1|
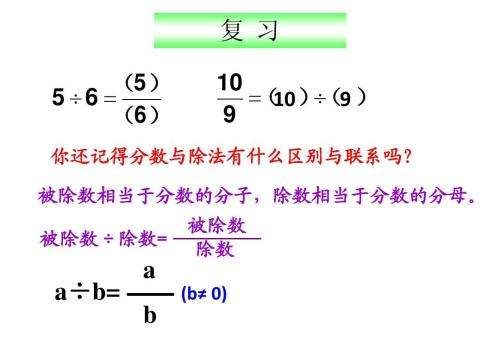
设圆半径为r,圆心为(m,n)
直线方程为ax+by+c=0
弦心距为d
则d^2=(ma+nb+c)^2/(a^2+b^2 )
则弦长的一半的平方为(r^2-d^2)/2
弦长公式,在这里指直线与圆锥曲线相交所得弦长d的公式。
圆锥曲线, 是数学、几何学中通过平切圆锥(严格为一个正圆锥面和一个平面完整相切)得到的一些曲线,如:椭圆,双曲线,抛物线等。
扩展资料:
直线与圆锥曲线的位置关系是平面解析几何的重要内容之一,也是高考的热点,反复考查。考查的主要内容包括:直线与圆锥曲线公共点的个数问题;弦的相关问题(弦长问题、中点弦问题、垂直问题、定比分点问题等);对称问题;最值问题、轨迹问题和圆锥曲线的标准方程问题等。
设而不求的思想方法对于求直线与曲线相交弦长是十分有效的,然而对于过焦点的圆锥曲线弦长求解利用这种方法相比较而言有点繁琐,利用圆锥曲线定义及有关定理导出各种曲线的焦点弦长公式就更为简捷。
如何算弦长公式
直线与椭圆相交的弦长公式是:弦长=│y1-y2│√【(1/k²)+1】。
圆的弦长是圆心角所对的弦与圆心连线(即圆上的点到圆心的距离)。
弦长=2Rsina,R是半径,a是圆心角;弦长为连接圆上任意两点的线段的长度。弦长公式,在这里指直线与圆锥曲线相交所得弦长的公式。圆锥曲线,是数学、几何学中通过平切圆锥(严格为一个正圆锥面和一个平面完整相切)得到的些曲线,如:椭圆,双曲线,抛物线等。
关于直线与圆锥曲线相交求弦长,通用方法是将直线y=kx+b代入曲线方程,化为关于x(或关于y)的一元二次方程,设出交点坐标。
直线与圆锥曲线的位置关系是平面解析几何的重要内容之一,也是高考的热点,反复考查。考查的主要内容包括:直线与圆锥曲线公共点的个数问题。
弦的相关问题(弦长问题、中点弦问题、垂直问题、定比分点问题等);对称问题;最值问题、轨迹问题和圆锥曲线的标准方程问题等。
利用韦达定理及弦长公式求出弦长,这种整体代换,设而不求的思想方法对于求直线与曲线相交弦长是十分有效的,然而对于过焦点的圆锥曲线弦长求解利用这种方法相比较而言有点繁琐,利用圆锥曲线定义及有关定理导出各种曲线的焦点弦长公式就更为简捷。
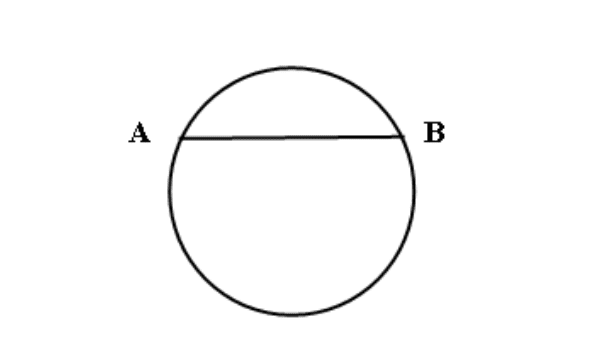
直线和圆位置关系:
1、直线和圆无公共点,称相离。AB与圆O相离,d(圆心到直线的距离)>r(半径)。
2、直线和圆有两个公共点,称相交,这条直线叫做圆的割线。即AB与⊙O相交,d 3、直线和圆有且只有一公共点,称相切,这条直线叫做圆的切线,这个公共点叫做切点。圆心与切点的连线垂直于切线。AB与⊙O相切,d=r。 以上就是关于解析几何弦长公式,弦长公式怎么推导出来的的全部内容,以及解析几何弦长公式的相关内容,希望能够帮到您。 版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。