lnx在1到e上的积分是多少
lnx在1到e上的积分是1,原式=∫(1,e)lnxdx=xlnx(1,e)-∫(1,e)xdlnx=xlnx(1,e)-∫(1,e)x*1/xdx=xlnx(1,e)-∫(1,e)dx=(xlnx-x)(1,e)=(e-e)-(0-1)=1。
定积分是积分的一种,是函数f(x)在区间[a,b]上的积分和的极限。这里应注意定积分与不定积分之间的关系:若定积分存在,则它是一个具体的数值(曲边梯形的面积),而不定积分是一个函数表达式,它们仅仅在数学上有一个计算关系(牛顿-莱布尼茨公式),其它一点关系都没有!
定积分中x从到e所围的面积为多少怎么求
所围面积为1.
解析:
围的面积x是从1积分到e;
所以定积分∫[1,e]lnxdx;
=xlnx[1,e]-∫[1,e]dx;
=e-(e-1);
=1;
所以所围面积为1。
黎曼积分
定积分的正式名称是黎曼积分。用黎曼自己的话来说,就是把直角坐标系上的函数的图象用平行于y轴的直线把其分割成无数个矩形,然后把某个区间[a,b]上的矩形累加起来,所得到的就是这个函数的图象在区间[a,b]的面积。实际上,定积分的上下限就是区间的两个端点a,b。
我们可以看到,定积分的本质是把图象无限细分,再累加起来,而积分的本质是求一个导函数的原函数。
定义法求ex的积分
∫[1,e]lnxdx
=xlnx|[1,e]-∫[1,e]x*1/x*dx
=e-x|[1,e]
=e-(e-1)
=1
lnx/1的积分是多少
lnx的积分是:x ln (x) -x +C,(C为任意常数)。
解题过程如下:
∫ ln (x) dx
=x ln (x) -∫ x d [ ln(x) ]
=x ln(x) -∫ x *(1/x) dx
=x ln (x) -∫ dx
=x ln (x) -x +C,(C为任意常数)
在微积分中,一个函数f 的不定积分,或原函数,或反导数,是一个导数等于f 的函数 F ,即F ′ = f。
不定积分和定积分间的关系由微积分基本定理确定。其中F是f的不定积分。
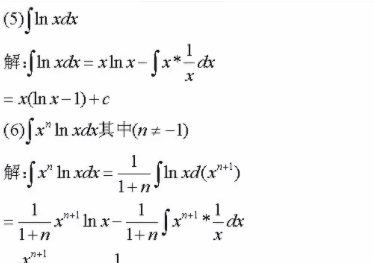
e与π的哲学意义:
数学讲求规律和美学,可是圆周率π和自然对数e那样基本的常量却那么混乱,就如同两个“数学幽灵”。人们找不到π和e的数字变化的规律,可能的原因:例如:人们用的是十进制,古人掰指头数数,因为是十根指头,所以定下了十进制,而二进制才是宇宙最朴素的进制,也符合阴阳理论,1为阳,0为阴。
再例如:人们把π和e与那些规整的数字比较,所以觉得e和π很乱,因此涉及“参照物”的问题。那么,如果把π和e都换算成最朴素的二进制,并且把π和e这两个混乱的数字相互比较,就会发现一部分数字规律,e的小数部分的前17位与π的小数部分的第5-21位正好是倒序关系,这么长的倒序,或许不是巧合。
lnx的积分和lnx的平方的积分
答:
∫(1到e)lnxdx=(xlnx-x)|(1到e)=elne-e-ln1+1=1
∫(1到e)(lnx)²dx=[x(lnx)²-2xlnx+2x]|(1到e)=e(lne)²-2elne+2e-(ln1)²+2ln1-2=e-2<1
所以∫(1到e)lnxdx > ∫(1到e)(lnx)²dx
以上就是关于lnx在到e上的积分是多少的全部内容,以及lnx在1到e上的积分是多少的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。