贝叶斯公式的通俗解释
贝叶斯法则通俗解释是:通常,事件A在事件B(发生)的条件下的概率,与事件B在事件A的条件下的概率是不一样的;然而,这两者是有确定的关系,贝叶斯法则就是这种关系的陈述。
贝叶斯定理由英国数学家贝叶斯发展,用来描述两个条件概率之间的关系,比如P(A|B)和P(B|A)。按照乘法法则,可以立刻导出:P(A∩B)=P(A)*P(B|A)=P(B)*P(A|B)。如上公式也可变形为:P(A|B)=P(B|A)*P(A)/P(B)。
贝叶斯概率公式例题
贝叶斯概率公式的理解:P(A|B) 和 P(B|A),按照乘法法则,可以立刻导出:P(A∩B) = P(A)*P(B|A)=P(B)*P(A|B)。公式也可变形为:P(A|B)=P(B|A)*P(A)/P(B)。
贝叶斯概率公式的详细解析:
P(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
P(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
P(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
P(B)是B的先验概率或边缘概率,也作标准化常量。
贝叶斯概率公式的定义:
指当分析样本大到接近总体数时,样本中事件发生的概率将接近于总体中事件发生的概率。但行为经济学家发现,人们在决策过程中往往并不遵循贝叶斯规律,而是给予最近发生的事件和最新的经验以更多的权值,在决策和做出判断时过分看重近期的事件。

贝叶斯概率公式的意义和偏差的定义:
偏差的定义:
面对复杂而笼统的问题,人们往往走捷径,依据可能性而非根据概率来决策。这种对经典模型的系统性偏离称为“偏差”。
由于心理偏差的存在,投资者在决策判断时并非绝对理性,会行为偏差,进而影响资本市场上价格的变动。但长期以来,由于缺乏有力的替代工具,经济学家不得不在分析中坚持贝叶斯法则。
贝叶斯概率公式的意义:
贝叶斯公式为利用搜集到的信息对原有判断进行修正提供了有效手段。在采样之前,经济主体对各种假设有一个判断(先验概率)。
关于先验概率的分布,通常可根据经济主体的经验判断确定(当无任何信息时,一般假设各先验概率相同),较复杂精确的可利用包括最大熵技术或边际分布密度以及相互信息原理等方法来确定先验概率分布。
一个简单例子理解贝叶斯公式的方法
一个简单例子理解贝叶斯公式具体解释如下:
1、贝叶斯公式
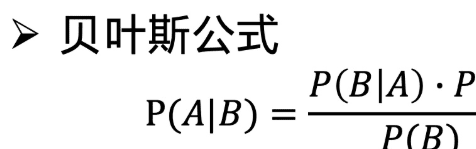
如上图公式所示,其中,各个概率P所对应的事件:
P(A)是A发生的概率;
P(B)是B发生的概率;
P(A|B)是在B发生的情况下A发生的概率;
P(B|A)是在A发生的情况下B发生的概率。
贝叶斯公式的推导在于理解事件A发生且事件B发生的概率。P(A∩B)其可以描述为:
P(A∩B)=P(A)*P(B|A)。
PA∩B)=P(B)*P(A|B)。
可以看出,贝叶斯公式用来描述两个条件概率之间的关系:P(A|B)和P(B|A)。
通常贝叶斯公式可以用来求在已知其他事件概率P(B|A)的情况下求目标事件概率(P(A|B)。
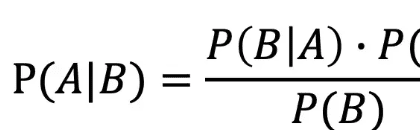
2、贝叶斯公式的应用
比如一间房屋在过去1年共发生过3次被盗事件;房屋有一条狗,狗平均每天晚上叫1次;若假设在盗贼入侵时狗叫的概率为0.9,则狗叫时发生盗贼入侵的概率是多少?
按照事件概率的形式描述如下:
P(A):狗每天叫的事件概率为1;
P(B):盗贼入侵事件的概率为3/365≈0.008;
P(A|B):盗贼入侵时狗叫的概率为0.9。
P(B|A):狗叫时盗贼入侵的概率?
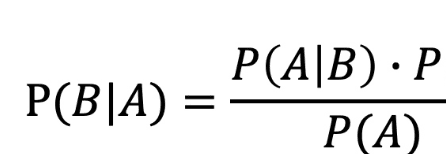
根据贝叶斯公式,即可求得:
P(B|A)=0.9*0.008/1=0.0072。
以上就是关于贝叶斯概率公式例题,贝叶斯公式的通俗解释的全部内容,以及贝叶斯公式的通俗解释的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。