角边角用字母怎么表示
角边角用字母表示是ASA。两角及其夹边对应相等的两个三角形全等,简称“角边角”,若有角边角现象,可证明两个三角形全等,证出两个三角形全等后,还可知道对应角相等,对应线段相等。
三角形是由同一平面内不在同一直线上的三条线段“首尾”顺次连接所组成的封闭图形,在数学、建筑学有应用。常见的三角形按边分有普通三角形(三条边都不相等),等腰三角(腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形);按角分有直角三角形、锐角三角形钝角三角形等,其中锐角三角形和钝角三角形统称斜三角形。
角有哪几种表示方法图解
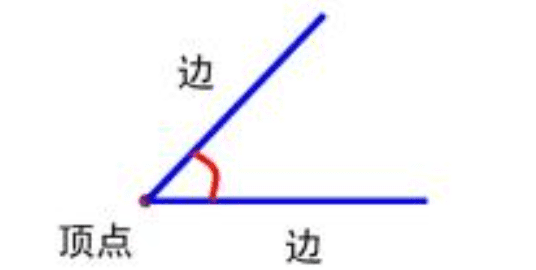
角的记法
1、用三个大写英文字母表示,例:∠AOC(顶点写在中间)
2、用一个大写英文字母表示,例:∠O
3、用数字表示,例:∠1
3、用1个希腊字母表示,例:∠β
角的平分线定理
1、角平分线上的点到角两边的距离相等。
2、若角内部一点到角两边的距离相等,则该点在这个角的角平分线上。
扩展资料:
角的性质
对称性:角具有对称性,对称轴是角的角平分线所在的直线。
角的平分线
定义:从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。
相关定理:
1.性质定理:角平分线上的点到角两边的距离相等。
2.判定定理:到角的两边距离相等的点在这个角的平分线上。
参考资料
角边角用什么字母表示
边角边用字母SAS表示。
边角边相关介绍:
边角边(SAS):有两边和它们的夹角对应相等的两个三角形全等简写成 边角边(SAS)。
把△ABC放到△A'B'C'上,使角A的顶点与角A'的顶点重合,由于角A=角A',因此可以使射线AB,AC分别落在射线A'B',C'A'上因为AB=A'B',AC=A'C',所以点B,C分别与点B',C'重合,这样△ABC与△A'B'C'重合,即△ABC全等于△A'B'C'。

题型:
三角形DEF的顶点D在三角形ABC的边BC上(不与B 、C 重合),且∠BAC+∠EDF=180度,AB=DF,AC=DE,点O 为EF 的中点。直线DO 交直线AB 于点P。
⑴猜想∠BPD 与∠FDB 的关系,并加以证明;
⑵当△DEF 绕点D 旋转,其他条件不变,⑴中的结论是否始终成立?若成立,请你写出真命题;若不成立请你再画出相应的图形,并给出正确的结论(不需要证明)。
证明:
分别作E,F关于D为对称中心的对称点G,H; 并连EG,FH,
∵EH,FG互相平分于D点,∴E,F,H,G 构成平行四边形,
∵QD为△FEG的中位线,∴QD//EG ,∴∠QDF=∠EGD,
又∵ED=AC,DG=DF=AB,∠EDG=180°-∠EDF=∠BAC,
∴△GDE≌△BAC ∴∠EGD=∠ABC,
即∠QDF=∠ABC,
∠BDF=∠QDB+∠QDF=180°-∠ABC-∠BPD+∠ABC,
∴∠BDF+∠BPD=180°,
在上述证明过程中,D在三角形ABC的边BC上(不与B 、C 重合)。
只要DQ不与AB平行,∠BPD总是存在,现令DQ//AB时, ∠BPD=0°,
GF与BC重合,即B,D,F共线, 令∠BDF=180°。
∴∠BDF+∠BPD=180°,
因此,当三角形DEF 绕点D 旋转,其他条件不变, ∠BDF+∠BPD=180°结论始终成立。
边角边的字母缩写是什么
边:S 角:A
边边边(SSS)
角角角(AAA)
边边角(SSA)
角角边(AAS)
边角边(SAS)
角边角(ASA)
斜边直角边(HL)
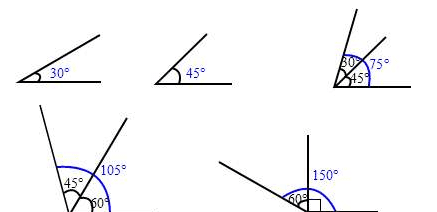
角的三种表示方法
一、角本身的表示方法:
1、用表示角的边和顶点的字母表示,如角AOB;
2、用单个希腊字母或数字表示角;
3、用两个向量表示角。
二、角的大小的表示方法:
1、角度制;
2、弧度制;
3、密位(360度=6000密位,军事上用得多);
4、把一个圆周均分成400分,其中的一份位1 GRAD 日本用得多
扩展资料:
角的大小与边的长短没有关系;角的大小决定于角的两条边张开的程度,张开的越大,角就越大,相反,张开的越小,角则越小。在动态定义中,取决于旋转的方向与角度。角可以分为锐角、直角、钝角、平角、周角、负角、正角、优角、劣角、零角这10种。以度、分、秒为单位的角的度量制称为角度制。此外,还有密位制、弧度制等。
以上就是关于角边角用字母怎么表示,角有哪几种表示方法图解的全部内容,以及角边角用字母怎么表示的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。