0的实部和虚部是什么，实部虚部指的是什么坐标

0的实部和虚部是什么

0的实部和虚部都是0。0是-1与1之间的整数。0既不是正数，也不是负数;0不是质数。0是偶数。在数论中，0属于自然数，0没有倒数；0的相反数是0；在集合论和计算机科学中，0属于自然数。

对于复数z=x+iy，其中x，y是任意实数，y称为复数z的虚部。y=Imz。在笛卡尔直角坐标系中，y轴的值为虚部。利用实部和虚部可以判断两个复数是否相等，定义共轭复数，计算复数的模和辐角主值。

在数学中，复数可以表示为实部和虚部的形式。一个复数的实部和虚部分别是由实数和虚数构成的。

实部指的是一个复数的实数部分，也就是复数在实数轴上的投影长度。实部通常用英文单词“real part”来表示，记作Re(z)。

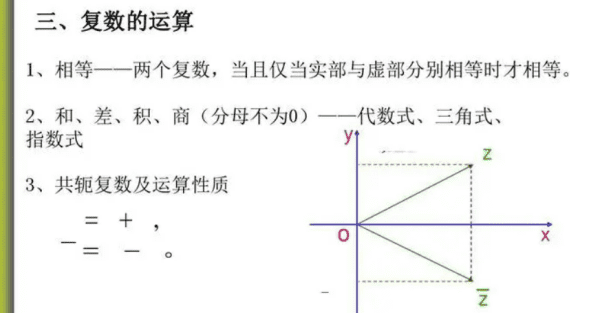
虚部指的是一个复数的虚数部分，也就是复数在虚数轴上的投影长度。虚部通常用英文单词“imaginary part”来表示，记作Im(z)。

假设一个复数z=a+bi，其中a和b均为实数，那么它的实部是a，虚部是b，可以表示为：Re(z)=a，Im(z)=b。

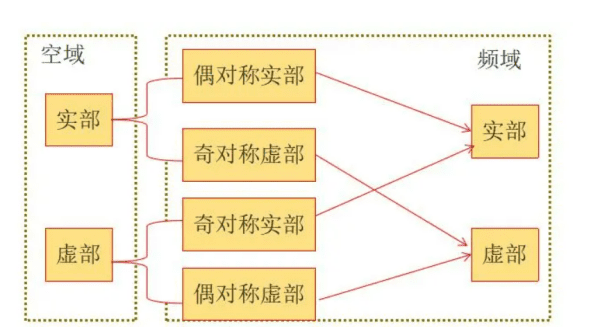
总之，实部和虚部是用来表示复数中实部和虚部的概念。复数的实部和虚部是通过复数的实部和虚部运算得到的，实部和虚部在代数学和物理学中具有广泛的应用，如在电路、信号处理、量子力学等方面。

实部与虚部是数学名词“复数”中的一个概念，把形如z=a+bi（a，b均为实数）的数称为复数，其中a称为实部，b称为虚部，i称为虚数单位。

相关介绍：

当z的虚部等于零时，常称z为实数；当z的虚部不等于零时，实部等于零时，常称z为纯虚数。复数域是实数域的代数闭包，即任何复系数多项式在复数域中总有根。

复数是由意大利米兰学者卡当在十六世纪首次引入，经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，此概念逐渐为数学家所接受。

扩展资料

复数的加法法则：设z1=a+bi，z2=c+di是任意两个复数。两者和的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。两个复数的和依然是复数。

复数的乘法法则：把两个复数相乘，类似两个多项式相乘，结果中i2= -1，把实部与虚部分别合并。两个复数的积仍然是一个复数。

利用傅立叶变换可将实信号表示成一系列周期函数的和。这些周期函数通常用形式如下的复函数的实部表示。

1.复数的实部在坐标系上是只存在在x轴上的点,虚部是只存在在y轴上的点。

2. 我们把形如 z=a+bi（a、b均为实数）的数称为复数。

3.其中，a 称为实部，b 称为虚部，i 称为虚数单位。

4.当 z 的虚部 b＝0 时，则 z 为实数；当 z 的虚部 b≠0 时，实部 a＝0 时，常称 z 为纯虚数。

5.复数域是实数域的代数闭包，即任何复系数多项式在复数域中总有根。

6. 复数是由意大利米兰学者卡当在16世纪首次引入，经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，此概念逐渐为数学家所接受。

2+3i，8-4i，6，i，7i，0均为复数，

2+3i的实部为2，虚部为3；

8-4i的实部为8，虚部为-4；

6的实部为6，虚部为0；

i的实部为0，虚部为1；

7i的实部为0，虚部为7；

0的实部和虚部均为0．

以上就是关于0的实部和虚部是什么，实部虚部指的是什么坐标的全部内容，以及0的实部和虚部是什么的相关内容,希望能够帮到您。