一元二次方程顶点坐标公式是什么
一元二次方程顶点坐标:[-b/2a,(4ac-b?)/4a]。顶点坐标是用来表示二次函数抛物线顶点的位置的参考指标,顶点式:y=a(x-h)?+k(a≠0,k为常数)。
只含有一个未知数(一元),并且未知数项的最高次数是2(二次)的整式方程叫做一元二次方程。一元二次方程经过整理都可化成一般形式ax?+bx+c=0(a≠0)。其中ax?叫作二次项,a是二次项系数;bx叫作一次项,b是一次项系数;c叫作常数项。成立条件如下:
①是整式方程,即等号两边都是整式,方程中如果有分母;且未知数在分母上,那么这个方程就是分式方程,不是一元二次方程,方程中如果有根号,且未知数在根号内,那么这个方程也不是一元二次方程(是无理方程)。
②只含有一个未知数。
③未知数项的最高次数是2。
一元二次方程的顶点坐标公式是啥
一元二次方程顶点坐标:[-b/2a,(4ac-b²)/4a]。顶点坐标是用来表示二次函数抛物线顶点的位置的参考指标,顶点式:y=a(x-h)²+k(a≠0,k为常数)。
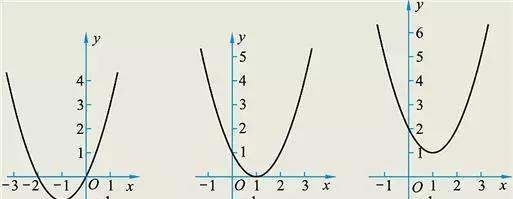
一元二次方程的应用
增长率问题;行程问题;经济问题;工程问题。一元二次方程是只含有一个未知数,且未知数的最高次数是二次的多项式方程,一元二次方程经过整理都可化成一般形式ax²+bx+c=0(a≠0)。
列方程解应用题的基本步骤:
1、审:审题。
2、找:找出题中的量,分清有哪些已知量、未知量,哪些是要求的未知量和所涉及的基本数量关系、相等关系。
3、设:设元,包括设直接未知数或间接未知数。
4、表:用所设的未知数字母的代数式表示其他的相关量。
5、列:列方程。
6、解:解方程。
7、检验:注意根的准确性及是否符合实际意义。
一元二次方程的顶点坐标公式是啥
一元二次方程顶点坐标:[-b/2a,(4ac-b²)/4a]。
顶点坐标是用来表示二次函数抛物线顶点的位置的参考指标,顶点式:y=a(x-h)²+k(a≠0,k为常数)。

一元二次方程介绍
只含有一个未知数(一元),并且未知数项的最高次数是2(二次)的整式方程叫做一元二次方程。一元二次方程经过整理都可化成一般形式ax+bx+c=0(a≠0)。其中ax叫作二次项,a是二次项系数;bx叫作一次项,b是一次项系数;c叫作常数项。成立条件如下:
①是整式方程,即等号两边都是整式,方程中如果有分母;且未知数在分母上,那么这个方程就是分式方程,不是一元二次方程,方程中如果有根号,且未知数在根号内,那么这个方程也不是一元二次方程(是无理方程)。
②只含有一个未知数。
③未知数项的最高次数是2。
一元二次方程的顶点坐标公式是啥
一元二次方程顶点坐标公式是:y=a(x-h)²+k(a≠0,a、h、k为常数),顶点坐标:(h,k)。
推导过程:
y=ax^2+bx+c
y=a(x^2+bx/a+c/a)
y=a(x^2+bx/a+b^2/4a^2+c/a-b^2/4a^2)
y=a(x+b/2a)^2+c-b^2/4a
y=a(x+b/2a)^2+(4ac-b^2)/4a
对称轴x=-b/2a
顶点坐标(-b/2a,(4ac-b^2)/4a)

一元二次方程:
仅包含一个未知数(一元)且未知项的最大次数为2(二次)的整式方程称为一元二次方程。一元二次方程经过整理都可化成一般形式ax²+bx+c=0(a≠0)。在这些条件下,ax²被称为二次项,a是二次项系数,b是次项,c被称为次项系数。
成立条件如下:
整式方程,即等号两侧为整式。如果方程中有分母;而且未知数在分母上,那么这个方程就是分式方程,而不是一元二次方程。如果方程中有根号,未知数在根号内,那么这个方程就不是一元二次方程(无理方程)。
1、只含有一个未知数。
2、未知数项的最高次数是2。
一元二次方程的顶点式怎么求
一元二次方程极值点公式:
顶点坐标:(-b/(2a),(-b2+4ac)/(4a2))
y=ax2+bx+c
=a(x2+bx/a+c/a)
=a
=a(x+b/2a)2-(b2-4ac)/4a2
当x=-b/2a时y=-(b2-4ac)/4a2
定义
一般地,自变量x和因变量y之间存在如下关系:
一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数
顶点式:y=a(x-h)2+k(a≠0,a、h、k为常数)
交点式(与x轴):y=a(x-x1)(x-x2)(a≠0,x1、x2为常数)
重要知识:a,b,c为常数,a≠0,且a决定函数的开口方向,a>0时,开口方向向上,a<0时,开口方向向下。IaI还可以决定开口大小,IaI越大开口就越小,IaI越小开口就越大。
二次函数表达式的右边通常为二次。
x是自变量,y是x的二次函数,当b2-4ac>0时:
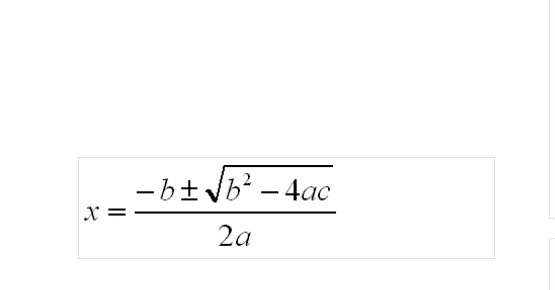
当b2-4ac=0时:x1=x2=-b/2a。
以上就是关于一元二次方程顶点坐标公式是什么的全部内容,以及一元二次方程顶点坐标公式是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。