复数的几何意义表示圆
复数的几何意义表示圆是z=(-1+2i)+z0=(-1+2cosθ)+(2+2sinθ)i,这是表示圆心在原点,半径等于2的圆的复数形式。
每一个复数有复平面内惟一的一个点和它对应,反过来,复平面内的每一个点,有惟一的一个复数和它对应,也就是复数的另一种表示方法,即几何表示方法。
数学题目
(一)由|z|≤1及|i(z)|≥1/2可知,复数z对应的点组成的平面图形是单位圆被两平行直线y=±1/2截得的上下两弓形,易知,弓形所对的圆心角为120º,弓高为1/2,弦长为√3,其面积=2×[(π/3)-(√3/4)]=(4π-3√3)/6.(二)因点p对应的复数为z1,而|z1|=2,故可设z1=2cost+2isint.(t∈r)===>2z1+3-4i=(4cost+3)+(4sint-4)i.由点q(x,y)对应2z1+3-4i,故x=4cost+3,y=4sint-4.消去参数t,可得点q的轨迹方程(x-3)²+(y+4)²=4².===>点q表示的图形是以点(3,-4)为圆心,半径为4的圆。
数学复数是什么意思
解答:
|z1-z2|的几何意义是z1,z2对应的两点间的距离
∴ |Z-i|表示z对应的点和i对应的点(0,1)两点间的距离
∵ |Z-i|=2表示z对应的点和i对应的点(0,1)两点间的距离恒为2
∴ z对应点的轨迹是以(0,-1)为圆心,2为半径的圆
复数的几何意义
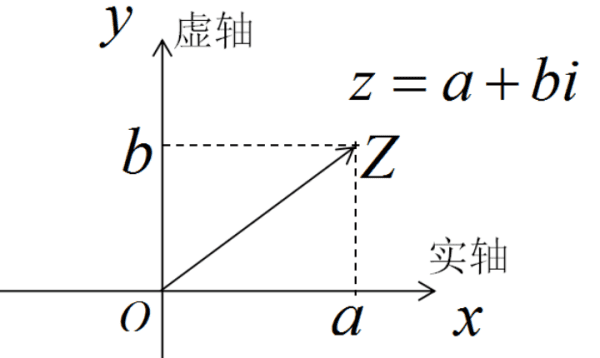
复数的几何意义,是指复数z=a+bi(a、b∈R),一一对应复平面内的点Z(a,b)。其中,在复平面内,复数的实部(a)是其对应点的横坐标,复数的虚部(b)是其对应点的纵坐标。
因为对于任何一个复数z=a+bi(a、b∈R),由复数相等的定义可知,可以由一个有序实数对(a,b)惟一确定,如z=3+2i可以由有序实数对(3,2)确定,又如z=-2+i可以由有序实数对(-2,1)来确定;又因为有序实数对(a,b)与平面直角坐标系中的点是一一对应的。由此可知,复数集与平面直角坐标系中的点集之间可以建立一一对应的关系。
点Z的横坐标是a,纵坐标是b,复数z=a+bi(a、b∈R)可用点Z(a,b)表示,这个建立了直角坐标系来表示复数的平面叫做复平面,也叫高斯平面,x轴叫做实轴,y轴叫做虚轴。实轴上的点都表示实数。对于虚轴上的点要除原点外,因为原点对应的有序实数对为(0,0), 它所确定的复数是z=0+0i=0表示是实数.故除了原点外,虚轴上的点都表示纯虚数。在复平面内的原点(0,0)表示实数0,实轴上的点(2,0)表示实数2,虚轴上的点(0,-1)表示纯虚数-i,虚轴上的点(0,5)表示纯虚数5i。非纯虚数对应的点在四个象限,例如点(-2,3)表示的复数是-2+3i,z=-5-3i对应的点(-5,-3)在第三象限等等。复数集C和复平面内所有的点所成的集合是一一对应关系。
german复数为什么是s
|z1-z2|的几何意义是,z1,z2对应点的距离
∴ |z+i|=1
即|z-(-i)|=1
是z对应的点和-i对应的点(0,-1)的距离等于1
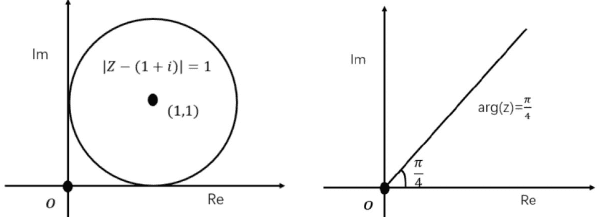
∴ 表示以(0,-1)为圆心,1为半径的圆.
以上就是关于数学题目,复数的几何意义表示圆的全部内容,以及复数的几何意义表示圆的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。



