双曲线的标准方程公式
双曲线的标准方程公式:焦点在X轴上时为:x?/a?-y?/b?=1(a>0,b>0);焦点在Y轴上时为:y?/a?-x?/b?=1(a>0,b>0)。
双曲线是指与平面上到两个定点的距离之差的绝对值为定值的点的轨迹,也可以定义为到定点与定直线的距离之比是一个大于1的常数的点之轨迹。
双曲线的标准方程a是什么
双曲线x²/a²-y²/b²=1,其中a代表双曲线顶点到原点的距离(实半轴),b代表双曲线的虚半轴,c代表焦点到原点的距离(半焦距),a,b,c满足关系式a²+b²=c²。
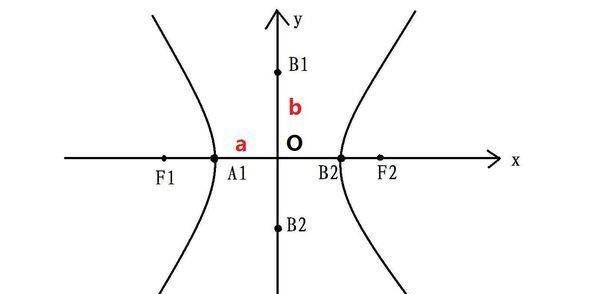
其中:OA1=a,OB1=b,OF1=c。O为原点。
我们把平面内与两个定点F1,F2的距离的差的绝对值等于一个常数(常数为2a,小于|F1F2|)的轨迹称为双曲线;平面内到两定点的距离差的绝对值为定长的点的轨迹叫做双曲线),即:│|PF1|-|PF2│|=2a。
相关信息:
双曲线的其他概念:
(1)A(-a,0),A'(a,0)。同时AA'叫做双曲线的实轴且│AA'│=2a。
(2)B(0,-b),B'(0,b)。同时BB'叫做双曲线的虚轴且│BB'│=2b。
(3)F1(-c,0)或(0,-c),F2(c,0)或(0,c)。F1为双曲线的左焦点,F2为双曲线的右焦点且│F1F2│=2c。
(4)离心率,第一定义:e=c/a且e∈(1,+∞)。
双曲线的标准方程a是什么
y=±(b/a)x(当焦点在x轴上),y=±(a/b)x (焦点在y轴上)(a:双曲线的实半轴,b是虚半轴。长)
几何性质:
(1)范围:|x|≥a,y∈R。
(2)对称性:双曲线的对称性与椭圆完全相同,关于x轴、y轴及原点中心对称。
(3)顶点:两个顶点A1(-a,0),A2(a,0),两顶点间的线段为实轴,长为2a,虚轴长为2b,且c2=a2+b2。与椭圆不同。
(4)渐近线:双曲线特有的性质,方程y=±(b/a)x(当焦点在x轴上),y=±(a/b)x (焦点在y轴上)或令双曲线。

渐近线特点:
无限接近,但不可以相交。分为垂直渐近线、水平渐近线和斜渐近线。
当曲线上一点M沿曲线无限远离原点时,如果M到一条直线的距离无限趋近于零,那么这条直线称为这条曲线的渐近线。
需要注意的是:并不是所有的曲线都有渐近线,渐近线反映了某些曲线在无限延伸时的变化情况。
根据渐近线的位置,可将渐近线分为三类:水平渐近线、垂直渐近线、斜渐近线。
y=k/x(k≠0)是反比例函数,其图象关于原点对称,x=0,y=0为其渐近线方程。
当焦点在x轴上时 双曲线渐近线的方程是y=[+(-)b/a]x。
当焦点在y轴上时 双曲线渐近线的方程是y=[+(-)a/b]x。
双曲线的一般方程式
双曲线的一般式和标准式,具体如下:
一、双曲式般式详标准形式:
1、双曲线的线方标准形式方程为:
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
其中,a和b都是标准正实数。双曲线的双曲式般式详中心在坐标系原点,a为双曲线横轴半轴长,线方b为双曲线纵轴半轴长。标准双曲线的双曲式般式详两支分别在x轴正半轴和x轴负半轴上,与y轴无交点。

2、标准一般形式:
双曲线的一般形式方程为:
$\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1$
其中,(h,k)为双曲线中心的坐标。这种形式的方程可以描述任意中心的双曲线,而不仅限于中心在坐标系原点的情况。
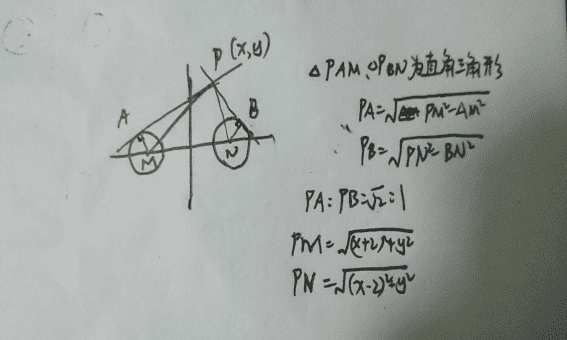
二、双曲线方程的两种形式分别的特点具体如下:
双曲线的标准形式方程描述了中心在坐标系原点的、横轴和纵轴半轴长分别为a和b的双曲线。这种形式的方程可以方便地计算出双曲线的各种性质和参数。而双曲线的一般形式方程则可以描述任意中心的双曲线,更加灵活。
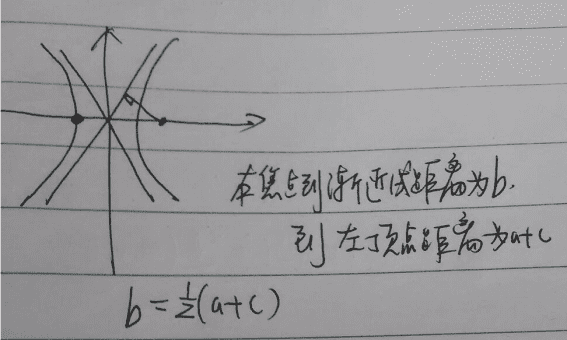
双曲线方程的应用和各种性质,具体如下:
1、双曲线方程的应用。
双曲线方程在解析几何、物理学、工程学、经济学等领域都有广泛的应用。例如,在物理学中,双曲线可以用来描述光线、粒子、电磁波等的运动轨迹;在工程学中,双曲线可以用来设计桥梁、隧道、建筑物等结构;在经济学中,双曲线可以用来描述市场需求和供给的关系等等。

2、双曲线方程确定双曲线的各种性质。
双曲线的各种性质包括中心、焦点、顶点、渐近线等等。通过双曲线方程,可以计算出双曲线的中心坐标、横轴和纵轴半轴长、焦点坐标等参数。另外,由于双曲线的渐近线方程为y=±(b/a)x,可以确定双曲线的两条渐近线的斜率和截距。
以上就是关于双曲线的标准方程公式,双曲线的标准方程a是什么的全部内容,以及双曲线的标准方程公式的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。




