abc中恰有一个发生怎么表示
表示abc中恰有一个发生是记A的补集为A“{至少有一个不发生}是{都发生}的补集,即(ABC)“(ABC)“=A“∪B“∪C“,在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件,简称事件。随机事件通常用大写英文字母A、B、C等表示。
随机事件是在一定条件下,可能发生,也可能不发生的事件。随机事件与确定性事件相比,是不确定的,因为对这种事件我们不能确定它是发生呢,还是不发生,即对事件的结果无法确定。
abc三个随机事件至少有一个发生
ABC三个随机事件至多有一个发生可表示为:
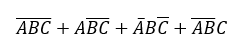
ABC三个随机事件至多有一个发生,即ABC均不发生或ABC三个随机事件恰好有一个发生,ABC三个随机事件恰好有一个发生又可以分为A发生且BC均不发生,B发生且AC均不发生,C发生且AB均不发生,这四个随机事件的或事件即ABC三个随机事件至多有一个发生的等价,可表示为上式。
拓展一下
ABC三个随机事件至多有一个发生,也可以理解为ABC中不可能有两个或以上的随机事件同时发生,从而也可表示为:
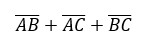
事件a、b、c中至少有两个发生可以表示成ab∪ac∪bc
如果x∈A∪B 那么有x∈A或者x∈B
也就是x至少在A和B其中之一
并集就是说构成它的子集至少有一个会发生
所以三个事件至少有一个发生就是把它们并起来
设abc为三个随机事件则事件至少有两个发生可表示为
PA*(1-PB)*(1-PC)+PB*(1-PA)(1-PC)+PC*(1-PA)(1-PB)
Pi表示发生第i件事的概率。
可表示为Pa(1-Pb)(1-Pc) + (1-Pa)Pb(1-Pc) + (1-Pa)(1-Pb)Pc。
解析:记Pa,Pb,Pc分别代表A,B,C发生的概率,那么可以看到:A,B,C恰发生一个可表示为Pa(1-Pb)(1-Pc) + (1-Pa)Pb(1-Pc) + (1-Pa)(1-Pb)Pc。
简介
随机事件是在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件(简称事件)。随机事件通常用大写英文字母A、B、C等表示。
随机试验中的每一个可能出现的试验结果称为这个试验的一个样本点,记作ωi。全体样本点组成的集合称为这个试验的样本空间,记作Ω.即Ω={ω1,ω2,…,ωn,…}。仅含一个样本点的随机事件称为基本事件,含有多个样本点的随机事件称为复合事件。
设a,b,c为三个事件,a,b,c至少一个不发生表示为( )
可表示为Pa(1-Pb)(1-Pc) + (1-Pa)Pb(1-Pc) + (1-Pa)(1-Pb)Pc。
解析:
记Pa,Pb,Pc分别代表A,B,C发生的概率,那么可以看到:A,B,C恰发生一个可表示为
Pa(1-Pb)(1-Pc) + (1-Pa)Pb(1-Pc) + (1-Pa)(1-Pb)Pc

扩展资料:
和事件(并事件)
称事件“A、B中至少有一个发生”为事件A和事件B的和事件,也称A与B的并,记作A∪B或A+B,A∪B发生意味着:或事件A发生,或事件B发生,或都发生。显然有:
①A⊂A∪B,B⊂A∪B;
②若A⊂B,A∪B=B
积事件(交事件)
称事件“A、B同时发生”为事件A与事件B的积事件,也称A与B的交,记作A∩B,简记为AB。事件AB发生意味着事件A发生且事件B也发生,也就是说A,B都发生。
显然有:
①AB⊂A,AB⊂B
②若A⊂B,则AB=A
随机事件特点:
1.可以在相同的条件下重复进行;
2.每个试验的可能结果不止一个,并且能事先预测试验的所有可能结果;
3.进行一次试验之前不能确定哪一个结果会出现。
以上就是关于abc中恰有一个发生怎么表示的全部内容,以及abc中恰有一个发生怎么表示的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。