不等式方程怎么解
不等式方程的解法是去分母、去括号、移项、合并同类项、系数化为1即可,一般地,用纯粹的大于号“>”、小于号“
通常不等式中的数是实数,字母也代表实数。两边的解析式的公共定义域称为不等式的定义域,不等式既可以表达一个命题,也可以表示一个问题。
解不等式方程怎么变号
求解不等式的步骤:
1、去分母;
2、去括号;
3、移项以及合并同类项;
4、系数化为一后进行求解。
注意事项:
1、不等式两边都乘以或除以一个负数,要改变不等号的方向;
2、 比两个值都大,就比大的还大,比两个值都小,就比小的还小;
3、不等式两边相加或相减,同一个数或式子,不等号的方向不变,移项要变号;
4、不等式两边相加或相减,同一个数或式子,不等号的方向不变;
5、不等式两边乘或除以同一个负数,不等号的方向改变。
解不等式的方法和步骤
初中解不等式的方法步骤如下:
1、材料准备:草稿纸、签字笔、铅笔、红笔等学习用品。

2、确定不等式的类型
首先,确定给定不等式的类型。常见的不等式类型包括一元一次不等式、一元二次不等式、绝对值不等式等。

3、进行变量移项
将不等式中的所有项移动到一侧,使不等式左边为零或一个表达式。这样可以将不等式转化为等式的形式。

4、确定不等式的解集
通过分析等式部分的符号来确定不等式的解集。根据不等式符号(大于、小于、大于等于、小于等于)以及变量的范围,确定解的范围。
5、绘制数轴或解集图
如果需要可视化解集,可以在数轴上标记出解集的位置,或者在解集图中表示出解集的区域。
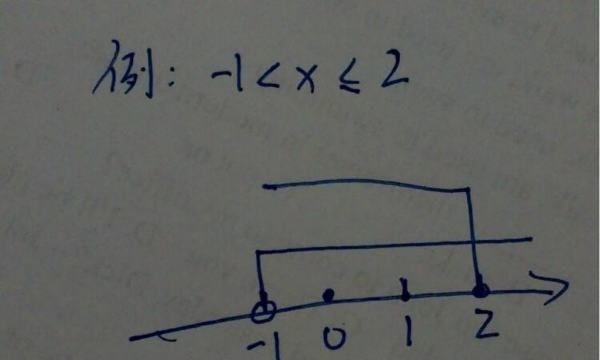
6、检验解的有效性
在解集确定后,可以选择一些特定的值代入原始不等式,检验解的有效性。确保解满足原始不等式,以验证解的正确性。

不等式方程可以分为以下几种类型:
1、一元一次不等式
这种不等式类似于一元一次方程,含有一个未知数,未知数的次数是1,未知数的系数不为0,左右两边为整式的不等式,例如:2x + 3 <5。
2、一元二次不等式
这种不等式含有一个未知数且未知数的最高次数为2的不等式,一般形式是 ax²+bx+c>0 、ax²+bx+c≠0、ax²+bx+c<0(a不等于0)。例如:x^2 - 4x > 3。
3、绝对值不等式
这种不等式是指一个数的绝对值与另一个数进行比较所得到的不等式。例如:|x + 2| ≤ 5。
4、分式不等式
分式不等式包含一个或多个未知数的分式,例如:(2x + 1)/(x - 3) > 0。
5、多元一次不等式
这种不等式包含两个或多个未知数和一次项,例如:3x + 2y ≤ 10。
6、系统不等式
包含多个不等式,通常有多个未知数,一般形式为F(x,y,……,z)≤G(x,y,……,z )(其中不等号也可以为 中某一个),两边的解析式的公共定义域称为不等式的定义域。例如:{x + y ≥ 5, 2x - y <3}。
一元二次不等式方程的解法
不等式方程的解法,包括一元一次不等式、一元一次方程、二元一次方程组和消元法。
一、一元一次不等式
一元一次不等式是指只含有一个未知数的一次不等式。它的解法通常采用如下步骤:
1、去分母:将不等式两边都乘以未知数的最高次项的系数,使不等式中的分数消去。
2、移项:将不等式两边同时加上或减去同一个数,使不等式中的某一项移到另一边。
3、合并同类项:将不等式两边相同次数的项合并在一起。
4、求得解集:根据不等号的方向,确定不等式的解集。
例如,解不等式2x-5>7。去分母:2x-5>7。移项:2x>7+5。合并同类项:2x>12求得解集:x>6。不等式的解集为 x>6。

二、一元一次方程
一元一次方程是指只含有一个未知数的一次方程。它的解法通常采用如下步骤:
1、移项:将方程两边同时加上或减去同一个数,使方程中的某一项移到另一边。
2、合并同类项:将方程两边相同次数的项合并在一起。
3、求得解:通过简单的运算,求得未知数的值。
例如,解一元一次方程3x-5=7,移项:3x=7+5,合并同类项:3x=12,求得解:x=4,所以,方程的解为x=4。

三、二元一次方程组
二元一次方程组是指含有两个未知数的一次方程组。它的解法通常采用消元法或代入法。
例如,解二元一次方程组:x+y=5,2x-y=1。
四、消元法
1、将第一个方程乘以2,得到新方程组:2x+2y=10和-y=-4。
2、将第二个方程和新方程组相加,消去 y,得到:3x=6。
3、 求得x=2,将x=2代入第一个方程,得到y=3。
所以,二元一次方程组的解为x=2, y=3。
以上就是关于不等式方程怎么解,解不等式方程怎么变号的全部内容,以及不等式方程怎么解的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。