为什么分式方程要检验
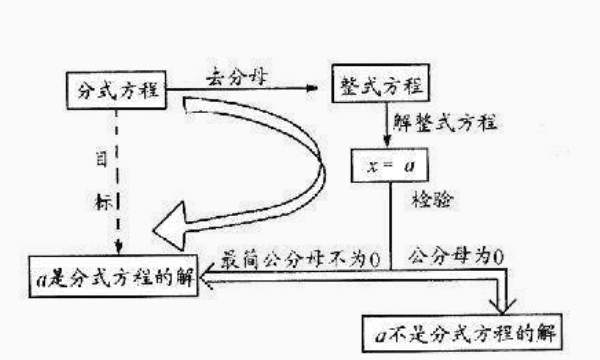
解分式方程检验的原因:因为在解分式方程时在两边同时乘了一个含有未知数的式子(最简公分母),所得方程和原方程不同解,有可能产生增根(使最简公分母=0的根),但这个增根并不是原方程的根。
检验的方法:验根时把整式方程的根代入最简公分母,如果最简公分母等于0,这个根就是增根。
否则这个根就是原分式方程的根。
若解出的根都是增根,则原方程无解。
一般的,解分式方程时,去分母后所得整式方程的解有可能使原方程中分母为零,因此要将整式方程的解代入最简公分母,如果最简公分母的值不为零,则是方程的解。
分式方程需要检验的原因
分式方程需要检验这件事情,是许多的中学生都知道的。并且在做分式方程的时候,其实也是需要去注意很多事项的,不然的话很有可能会导致最后的结果代入到方程中的时候是不符合的。因为分式方程本来就分为两个方程,所以说在解题的时候肯定会出现诸多的漏洞。那么如果不代入检验的话,很有可能就会造成其中一个答案是正确的,但是另一个答案是错误的。

需要不断寻找正确答案
所以说为了安全起见,也为了我们自己能够最终得到正确答案,检验是最重要的一步。在我们做完了一个分式方程之后,就需要去检验,并且也需要把这样的答案代入到这个方程当中,看看结果是否符合。很多人在带入之后就会发现其中一个答案是错误的,那么肯定是中间其中一个环节出现了差错,我们就需要重新去计算一半。这样的检验方式也能够让我们自己锻炼严谨的思维模式,能让我们自己在做题的时候更加的严谨,并且对于数字也更加的敏感。

要慢慢检查
其实在学习数学的时候,检验是非常重要的,对于一些理科方面的知识来说,检验才能够让我们自己不断的强化自己的记忆,而且能让我们自己在知识当中得到一定的规律。还有我们也会发现,检验了这一个方程之后,再解其他的一些方程的时候,我们就不需要再进行大量的计算,而是能够让我们自己直接就反应出来这一道题的答案。

所以说检验的确是非常的有帮助的,大家在做题的时候一定要注意细心。在做题的时候,我们自己一定要注意细心,这样才能够保证我们做题的时候会少出一些差错,也能够让我们自己的分数更加的高一些,这对于一个学生来说是至关重要的一个问题。
解分式方程为什么要验根
解分式方程检验的原因:求出未知数的值后必须验根,因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根。
检验的方法:验根时把整式方程的根代入最简公分母,如果最简公分母等于0,这个根就是增根。否则这个根就是原分式方程的根。若解出的根都是增根,则原方程无解。
如果分式本身约分了,也要代入进去检验。在列分式方程解应用题时,不仅要检验所得解的是否满足方程式,还要检验是否符合题意。
一般的,解分式方程时,去分母后所得整式方程的解有可能使原方程中分母为零,因此要将整式方程的解代入最简公分母,如果最简公分母的值不为零,则是方程的解。
扩展资料:
分式方程:含分式,并且分母中含未知数的方程——分式方程。
增根:分式方程的增根必须满足两个条件:
1、增根是最简公分母为0。
2、增根是分式方程化成的整式方程的根。
分式方程的解法:
1、能化简的先化简。
2、方程两边同乘以最简公分母,化为整式方程。
3、解整式方程。
4、验根。
注:解分式方程时,方程两边同乘以最简公分母时,最简公分母有可能为0,这样就产生了增根,因此分式方程一定要验根。
注意:
(1)注意去分母时,不要漏乘整式项。
(2)増根是分式方程去分母后化成的整式方程的根,但不是原分式方程的根。
(3)増根使最简公分母等于0。
(4)分式方程中,如果x为分母,则x应不等于0。
检验格式:
把x=a 带入最简公分母,若x=a使最简公分母为0,则a是原方程的增根。若x=a使最简公分母不为零,则a是原方程的根。
注意:可凭经验判断是否有解。若有解,带入所有分母计算:若无解,带入无解分母即可。
以上就是关于为什么分式方程要检验,分式方程需要检验的原因的全部内容,以及为什么分式方程要检验的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。







