排队问题减一公式
排队问题减一公式:(n-1-m)。共有A根火柴,先在第m根做上标记,然后在第n根上也划上记号,那么第m根和n根之间共有(n-1-m)根火柴。
设m是5,n为16,那么代表16前边有15根火柴,也就是16-1,和5之间有几根火柴,就是用16-1-5=10根。之所以要减1,是要把16本身排除。
排队中间有几人为什么减1
因为问题问的是“中间几个人”,比如小明排队13,小红18问中间几个人,问的是“中间几个人”,也就是不包括小明和小红,18-13这个算式结果包括小明,所以要减去小明“1”,就是他两中间的人数。
有些排队问题中包含诸如:前面、后面、左面、右面、之间等词语,这时候是不包括这个关键人物本身的。
如果题目说某某排在第几名的时候,就包括这个关键人物。

在计算队伍的人数的时候,可以借助画示意图。将关键人物用特殊符号作个标记,顺便在下方用简要文字备注。其他不是很关键的可以用小圆圈代替,如果中间数量较多一般用省略号表示。在计算人数的时候特别要注意被重复计算的人数,最后需要减去。
一年级数学排队问题教案
1、已知部分求整体(用加法):两个有几,两数相加再加一,两个第几,两数相加再减一,有几第几,两数相加不算一。
2、已知整体求部分(用减法):两个第几,大小相减再减一,从几到几,大小相减再加一,一共第几,大小相减再加一。
加法运算
1、同号两数相加,取与加数相同的符号,并把绝对值相加。
2、异号两数相加,若绝对值相等则互为相反数的两数和为0;若绝对值不相等,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
3、互为相反数的两数相加得0。
4、一个数同0相加仍得这个数。
5、互为相反数的两个数,可以先相加。
6、符号相同的数可以先相加。
7、分母相同的数可以先相加。
一年级数学排队问题专项训练
加一的情况是这样子的:
比如说小朋友排成一排小明的,前面有三个人,小明的后面有四个人问你,这一排一共有几个小朋友。
所以你需要用3+4+1,这个依旧是小明,因为前面三个人,后面三个人都没有,包括小明,所以在计算总人数的时候,要把小明算到里面。
减一的情况是这样子的:
一排小朋友从前面数小,明排第三个,从后面数小明排第四个问你一共有几个小朋友?
这种情况需要用3+4-1=6人,因为小明从前面数数了一遍,从后面数又数了一遍,所以3+4里面有两个小明要剪去,其中一个小明那就是六个人了。
小学数学是通过教材,教小朋友们关于数的认识,四则运算,图形和长度的计算公式,单位转换一系列的知识,为初中和日常生活的计算打下良好的数学基础。
荷兰教育家弗赖登诺尔认为:“数学来源于现实,也必须扎根于现实,并且应用于现实。”的确,现代数学要求我们用数学的眼光来观察世界,用数学的语言来阐述世界。
从小学生数学学习心理来看,学生的学习过程不是被动的吸收过程,而是一个以已有知识和经验为基础的重新建构的过程,因此,做中学,玩中学,将抽象的数学关系转化为学生生活中熟悉的事例,将使儿童学得更主动。
从我们的教育目标来看,我们在传授知识的同时,更应注重培养学生的观察、分析和应用等综合能力。
一年级数学排队问题教案
运算口诀:
1、已知部分求整体(用加法):两个有几,两数相加再加一,两个第几,两数相加再减一,有几第几,两数相加不算一。
2、已知整体求部分(用减法):两个第几,大小相减再减一,从几到几,大小相减再加一,一共第几,大小相减再加一。
必须要弄清排队的顺序、方向及作为标准的人(或物)的位置。在计算总人数的时候,作为标准的人(或者物)如果计算了两次,就要减去1;如果没有计算,反之要加上1.既不能重复,也不能遗漏。
解决这类问题的关键:巧用画图法,找出重复的部分再解答。先来给大家详细总结排队问题所涉及到的知识点:
要素:
(1)方向:前后、左右、头尾。
(2)关键词:有几个、第几个、A和B之间、从A到B。
方法:(1)定方向 (2)定位置 (3)标条件和标问题(4)看图列式。
例题:
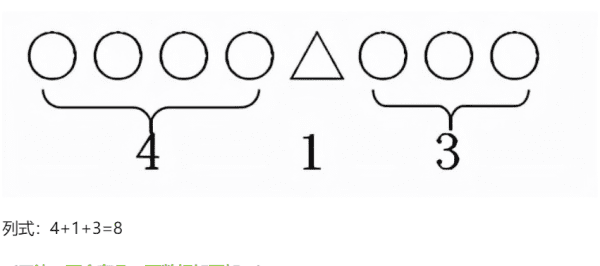
1、前面有4个人,后面有3个人,一共有多少人?
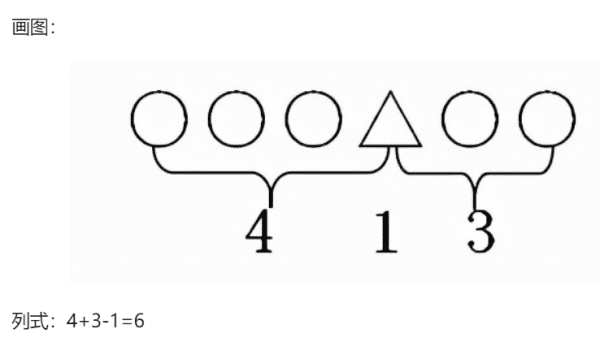
2、从前往后数排第4,从后往前数排第3,一共有多少人?
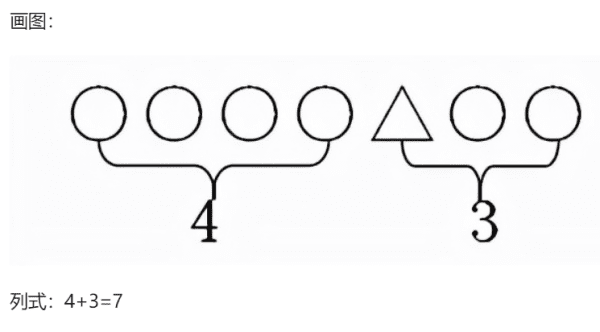
3、前面有4人,从后数排第3,一共有多少人?
在小学一年级的数学课程中,通常会对孩子们考察一类与生活结合紧密的数学问题,那就是我们常说的排队问题。这类问题的学习可以培养孩子们的数形结合能力,运用画图法解决实际问题的能力。
以上就是关于排队问题减一公式,排队中间有几人为什么减1的全部内容,以及排队问题减一公式的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。