怎么表示位置矢量
以坐标表示位置矢量,位置矢量是在某一时刻,以坐标原点为起点,以运动质点所在位置为终点的有向线段。
位移和位矢虽然都是矢量,但二者是两个不同的概念。
位矢是在某一时刻,以坐标原点为起点,以运动质点所在位置为终点的有向线段;而位移是在一段时间间隔内,从质点的起始位置引向质点的终止位置的有向线段。
大学物理:实际上位置矢量的定义并不需要一定有坐标系的存——怎么理解这句话
在大学物理中,位置矢量的定义是描述某个质点在空间中的位置和方向的矢量,通常用符号\vec{r}表示。位置矢量的定义并不需要一定有坐标系的存在,这是因为位置矢量是一个独立于坐标系的物理量,它只与质点在空间中的位置和方向有关。
具体来说,如果我们知道某个质点在空间中的位置和方向,我们就可以通过定义一个起点和一个方向来得到它的位置矢量,而不需要依赖于任何特定的坐标系。这个起点可以是任意的参考点,而方向则可以是任意的空间方向。例如,我们可以定义一个参考点为原点,然后定义一个方向为“向北”的向量,通过这个向量的长度和方向来表示质点在空间中的位置。这种方式下,我们并没有引入任何坐标系,而是直接使用了位置矢量来描述物体的位置。
当然,在实际问题中,通常需要建立坐标系来更方便地描述质点的位置和运动状态。此时,我们可以通过引入坐标系来将位置矢量表示为一组坐标数值,这样可以更方便地进行运算和分析。但这并不改变位置矢量作为一个物理量的本质定义,即描述质点在空间中位置和方向的矢量。
位置矢量怎么求
位置矢量的大小称为这个向量的模,数学上用两条竖线将空间向量包围来表示,定义为各个分向量的平方和,再开方。这在理解上不存在问题,就像高中学过的平面上两点的距离一样,都是先求平方和再开方。
既然位置矢量有方向,那就应该有一些物理量来表示其方位,一般是用角度来表示。三个角度就可以完整的求出其方位,在x轴上的角度的余弦的大小为x分量与向量的模相除的值,其他两个角度表示的方法一样。
位矢的第一个性质是矢量性,一个矢量应该包含有起点和终点,一个点的矢量是以这个点为终点,坐标原点为起点的。起点和终点相连,从起点指向终点的方向就是矢量的方向。
位矢的第二个性质是瞬时性,当一个质点发生移动时,哪怕是一个无穷小的移动,都会引起位矢大小和方向的变化。因为两点只能够确定一个位矢,当一个点发生过变化时,两个点的相对位置就会发生变化,所以位矢是每时每刻都在变化的。
位矢的第三个性质是相对性,位矢是依靠坐标系而存在的,在一个坐标系中确定的位矢,在另外一个坐标系中位矢的大小和方向都有可能发生改变。
如何用向量来表示点的位置和方向
平面向量八大定理:如果两个向量a、b不共线,那么向量p与向量a、b共面的充要条件是:存在唯一实数对x、y,使p=xa+yb。
有向线段的要素:起点,方向,长度。长度为零的向量为零向量,单位向量为一长度单位。方向相同或相反的非零向量为平行向量。
当两个方向相互垂直时,其实就是把他们在直角坐标系中分解,此时(x,y)就称为此向量的坐标。所以此定理为向量的坐标表示提供了理论依据。
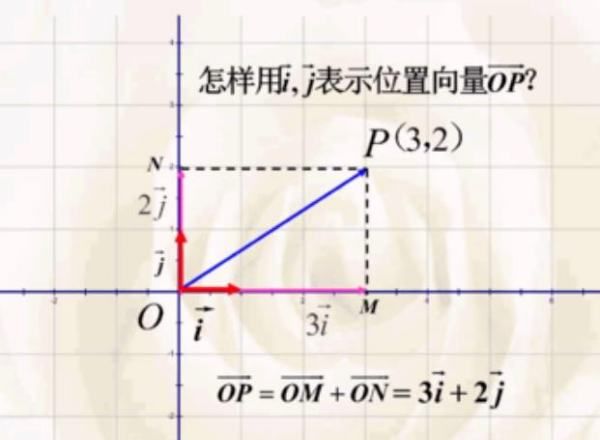
在平面直角坐标系中,分别取与x轴,y轴方向相同的两个单位向量i、j作为基底,a为坐标平面内的任意向量,以坐标原点O为起点作向量OP=a。有平面向量基本定理可知,有且只有一对实数x、y,使得向量OP=xi+yj。因此,a=xi+yj。
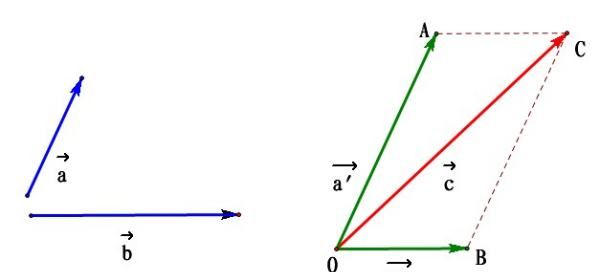
我们把实数(x,y)对叫做向量的坐标,记作:a=(x,y)。显然,其中(x,y)就是点P的坐标。向量OP称为点P的位置向量。平面向量的线性运算:加法为三角形法则'平行四边形法则'。定理:向量a与b共线,a不等于零,有且只有唯一一个实数c,使b=ca。
以上就是关于怎么表示位置矢量的全部内容,以及怎么表示位置矢量的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。