如何证明向量共面
设a,b,c是三个向量。要证a,b,c共面,只要证a,b,c的混合积为0,或者证其中一个可以由另外两个线性表示,例如:证存在实数x、y使得a=x·b+y·c。
共面定理的定义为能平移到一个平面上的三个向量称为共面向量。共面向量定理是数学学科的基本定理之一。属于高中数学立体几何的教学范畴。主要用于证明两个向量共面,进而证明面面垂直等一系列复杂定理。
三个向量共面有什么结论
要证明三个向量共面,可以使用以下两种方法之一:
向量叉乘法:设三个向量为a、b和c。如果它们共面,那么向量a和向量b的叉乘结果与向量c平行(或共线)。计算向量a和向量b的叉乘,得到一个新的向量d。如果向量d与向量c平行(或共线),则可以得出结论,三个向量共面。
行列式法:将三个向量a、b和c按列排列成一个3x3的矩阵A。计算矩阵A的行列式det(A)。如果det(A)等于零,那么可以得出结论,三个向量共面。
无论使用哪种方法,如果得出的结论是三个向量共面,那么它们就在同一个平面上。
怎么证明两个向量
怎么证明3个向量共面如下:
通过计算向量的混合积来判断:对于三维空间中的三个向量,如果它们的混合积为零,则这三个向量共面。2/5通过计算向量组的秩来判断:将三个向量排成一个矩阵,然后求矩阵的秩。如果矩阵的秩小于等于2,则这三个向量共面。
共面向量的定义:
能平移到一个平面上的三个向量称为共面向量。共面向量定理是数学学科的基本定理之一。属于高中数学立体几何的教学范畴。主要用于证明两个向量共面,进而证明面面垂直等一系列复杂问题。

如果两个向量a.b不共线,则向量p与向量a.b共面的充要条件是存在唯一有序实数对(x.y),使p=xa+yb定义为:能平移到同一平面上的三个向量叫做共面向量。
推论1:
设O、A、B、C是不共面的四点,则对空间任意一点P,都存在唯一的有序实数组(x,y,z)使得OP=xOA+yOB+zOC说明:若x+y+z=1则PABC四点共面。
(1)唯一性:设另有一组实数x',y',z'使得OP=x'OA+y'OB+z'OC则有xOA+yOB+zOC=x'OA+y'OB+z'OC∴(x-x')OA+(y-y')OB+(z-z')OC=0∵OA、OB、OC不共面∴x-x'=y-y'=z-z'=0即x=x'、y=y'、z=z'故实数x,y,z是唯一的。
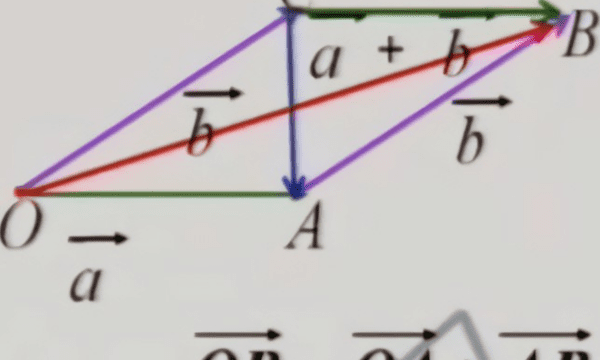
(2)若x+y+z=1,则PABC四点共面:
假设OP=xOA+yOB+zOC且x+y+z=1,且PABC不共面那么z=1-x-y,则OP=xOA+yOB+(1-x-y)OC=xOA-xOC+yOB-yOC+OC=OC+xCA+yCB(CP=xCA+yCB)点P位于平面ABC内,与假设中的条件矛盾,故原命题成立。
推论2:
空间任一点P位于平面MAB内的充要条件是:存在有序实数对{,x.y},使MP=xMA+yMB或对空间任一定点O,有OP=OM+xMA+yMB。
如何证明三个向量共面的条件
三个向量任意两两组合,求得的法向量平行。
共面定理的定义为能平移到一个平面上的三个向量称为共面向量。共面向量定理是数学学科的基本定理之一。属于高中数学立体几何的教学范畴。主要用于证明两个向量共面,进而证明面面垂直等一系列复杂定理。
扩展资料
共面向量定理:如果两个向量a,b不共线,则向量c与向量a,b共面的充要条件是:存在唯一的一对实数x,y,使c=ax+by
三向量共面,例如v,u,z三向量,那么其中任意一个可以表示为其它两个的某种线性组合,即,存在常数 a,b,使得 z = av + bu。
如果两个向量a.b不共线,则向量p与向量a.b共面的充要条件是存在有序实数对(x.y),使p=xa+yb
空间一点P位于平面MAB内的充要条件是存在有序实数对x.y,使MP=xMA+yMB {MP MA MB 都表示向量}或对空间任一定点O,有OP=OM+xMA+yMB {OP,OM,MA,MB表示向量}
以上就是关于如何证明向量共面,三个向量共面有什么结论的全部内容,以及如何证明向量共面的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。