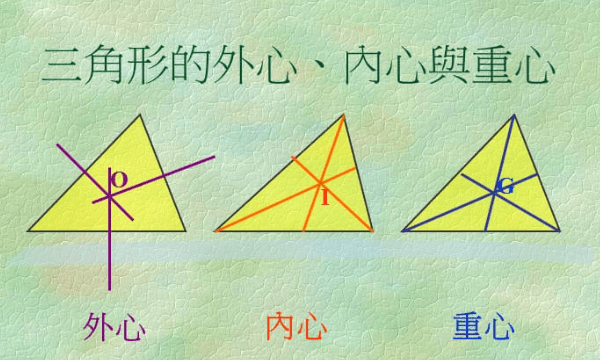
三角形的外心是什么线的交点
三角形的外心是三遍垂直平分线的交点,它到三角形三个顶点的距离相等,三角形外接圆的圆心叫做三角形的外心。三角形外接圆的圆心也就是三角形三边垂直平分线的交点,三角形的三个顶点就在这个外接圆上。
三角形的重心:三条边的中线交于一点。
三角形的垂心:三角形的三条高(所在直线)交于一点。
三角形的内心:三角形的三条内角平分线交于一点。
三角形的重心、外心、垂心、内心、旁心称为三角形的五心,它们都是三角形的重要相关点。旁心:三角形制一内角平分线和另外两顶点处的外角平分线交于一点。
外心是什么线的交点
1、外心是垂直平分线的交点。
2、三角形重心是三角形三边中线的交点。三角形的三条高线的交点叫做三角形的垂心。外心指三角形三条边的垂直平分线的相交点,用这个点做圆心可以画三角形的外接圆。内心是三角形三条内角平分线的交点,即内切圆的圆心。
外心是什么线的交点
外心是三角形三条中垂线的交点。
外心是一个数学名词。数学名词。指三角形三条边的垂直平分线(中垂线)的相交点。用这个点做圆心可以画三角形的外接圆。指三角形外接圆的圆心,一般叫三角形的外心。三角形的外心是三边中垂线的交点,且这点到三角形三顶点的距离相等。外心是三角形三条边的垂直平分线的交点,即外接圆的圆心。
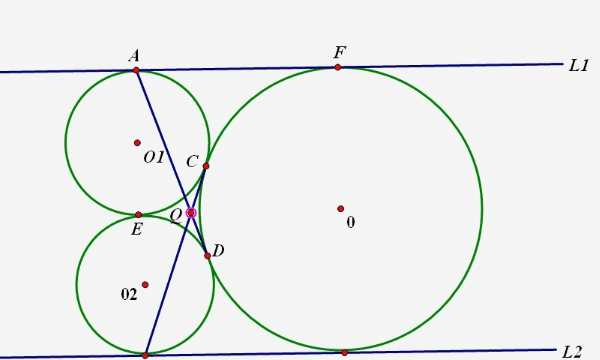
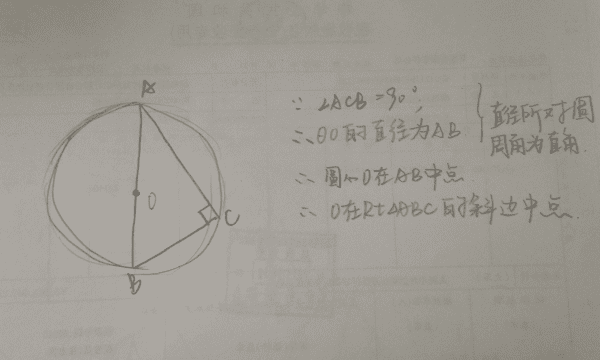
三角形外心的性质:锐角三角形的外心在三角形内; 直角三角形的外心在斜边上,与斜边中点重合; 钝角三角形的外心在三角形外。三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心,外心到三顶点的距离相等。
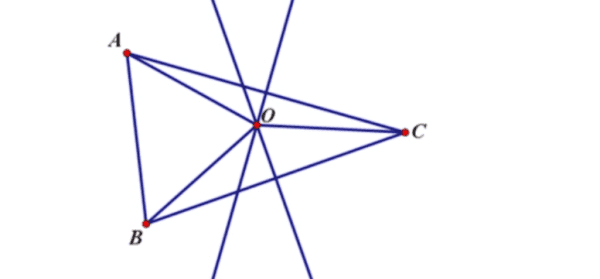
点G是平面ABC上一点,那么点G是⊿ABC外心的充要条件:(向量GA+向量GB)·向量AB= (向量GB+向量GC)·向量BC=(向量GC+向量GA)·向量CA=0。
性质
锐角三角形外心在三角形内部。直角三角形外心在三角形斜边中点。钝角三角形外心在三角形外。有外心的图形,一定有外接圆(各边中垂线的交点,叫做外心)。外接圆圆心到三角形各个顶点的线段长度相等。
过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心。在三角形中,三角形的外心不一定在三角形内部,可能在三角形外部(如钝角三角形)也可能在三角形边上(如直角三角形)。过不在同一直线上的三点可作一个圆(且只有一个圆)。
外心是三角形什么的交点
外心是三角形三条中垂线的交点。以外心为圆心,可以画出三角形的外接圆。指三角形外接圆的中心,一般称为三角形的外中心。三角形的外心是三条边的垂直线的交点,从这个点到三角形三个顶点的距离相等。震中是三角形三条边的垂直平分线的交点,即外接圆的中心。
三角形外心的性质有以下,性质一,锐角三角形的外心在三角形内部;直角三角形的外中心在斜边上,与斜边的中点重合;钝角的外心在三角形之外。性质二、三角形三条边的中垂线过一点,该点是三角形外接圆的圆心,外圆心到三个顶点的距离相等。
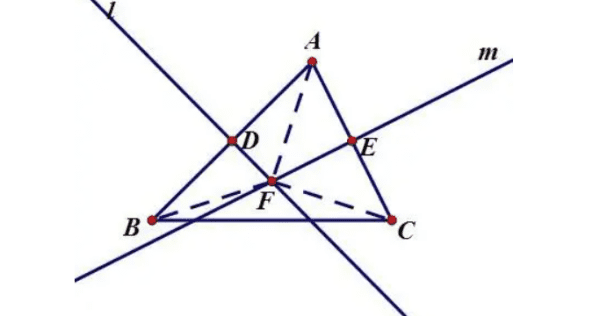
三角形的五心:重心:中线的交点 垂心:高(垂线)的交点 外心:三角形的外接圆的圆心,即边的垂直平分线的交点 内心:三角形的内接圆的圆心,即角平分线的交点 中心:即几何中心,主要是在中心对称图形中 三角形的重心,外心,垂心,内心和旁心称之为三角形的五心。三角形五心定理是指三角形重心定理、外心定理、垂心定理、内心定理,以及旁心定理的总称。
三角形外接圆的圆心是什么的交点坐标
三角形外接圆圆心叫做三角形的外心, 是三角形三边中垂线的交点,它到在整个顶点的距离相等, 三角形内切圆的圆心叫做三角形的内心,是三角形三个内角平分线的交点,它到三边的距离相等。
分别以线段两端为圆心,以大于线段1/2为半径在线段两侧作弧,连两相交点,此线就是该线段的垂直平分线。依据就是:线段的垂直平分线上任意一点,到线段两端的距离相等。
经过某一条线段的中点,并且垂直于这条线段的直线是线段的垂直平分线,到一条线段两个端点距离相等的点,在这条线段的垂直平分线上,即线段垂直平分线可以看成到线段两端点距离相等的点的集合。
与对称轴,若图形关于某条直线对称,这条轴就称为对称轴。以五角星为例,它有五条对称轴,垂直平分线是存在某条线段时才会有这个概念,它的定义是经过某一条线段的中点,并且垂直于这条线段的直线,叫作这条线段的垂直平分线。
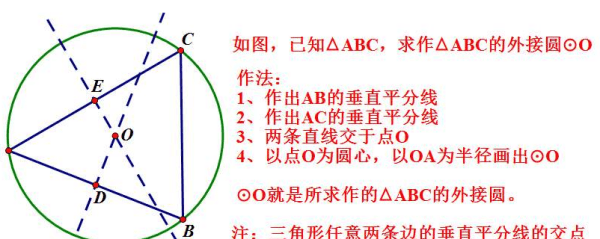
即做三角形三条边的垂直平分线。两条也可,两线相交确定一点。
以线段为例,可以看作是三角形一边。分别以两个端点为圆心适当长度(相等)为半径做圆(只画出与线段相交的弧即可),再分别以两交点为圆心,等长为半径(保证两圆相交)做圆,过最后的两个圆的两个交点做直线,这条直线垂直且平分这条线段即线段的垂直平分线。
以上就是关于外心是什么线的交点,三角形的外心是什么线的交点的全部内容,以及三角形的外心是什么线的交点的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。


