方程的解是什么意思，方程的解的定义是什么

方程的解的定义是什么

方程的解的定义是使方程左右两边相等的未知数的值。方程的解不唯一，解方程时，注意绝对值。只含有一个未知数的方程的解叫方程的根。x=2是方程2x-4=0的解，也是该方程的根。

方程是表示两个数学式（如两个数、函数、量、运算）之间相等关系的一种等式，是含有未知数的等式，通常在两者之间有一等号“=”。方程不用按逆向思维思考，可直接列出等式并含有未知数。具有多种形式，如一元一次方程、二元一次方程等。广泛应用于数学、物理等理科应用题计算。

方程的解是：

方程两边左右相等的未知数的值。

方程的解不唯一，解方程时，注意绝对值。

方程的解数学术语：

1、使得方程中等号两边相等的未知数的值叫做方程的解。

2、也可以说是方程中未知数的值叫做方程的解。

3、只含有一个未知数的方程的解叫方程的根。

4、x=2 是方程2x-4=0地解，也是该方程的根。

扩展资料：

方程解法：

一元三次方程的求根公式用通常的演绎思维是做不出来的，用类似解一元二次方程的求根公式的配方法只

能将型如ax^3+bx^2+cx+d+0的标准型一元三次方程形式化为x^3+px+q=0的特殊型。

一元三次方程的求解公式的解法只能用归纳思维得到，即根据一元一次方程、一元二次方程及特殊的高次方程的求根公式的形式归纳出一元三次方程的求根公式的形式。

归纳出来的形如 x^3+px+q=0的一元三次方程的求根公式的形式应该为x=A^（1/3）+B^（1/3）型，即为两个开立方之和。

1、含有未知数的等式叫方程，也可以说是含有未知数的等式是方程。

2、使等式成立的未知数的值，称为方程的解，或方程的根。

3、解方程就是求出方程中所有未知数的值的过程。

4、方程一定是等式，等式不一定是方程。不含未知数的等式不是方程。

5、验证：一般解方程之后，需要进行验证。验证就是将解得的未知数的值代入原方程，看看方程两边是否相等。如果相等，那么所求得的值就是方程的解。

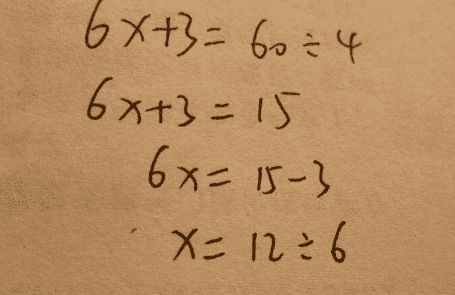
6、注意事项：写“解”字，等号对齐，检验。

7、方程依靠等式各部分的关系，和加减乘除各部分的关系（加数+加数=和，和-其中一个加数=另一个加数，差+减数=被减数，被减数-减数=差，被减数-差=减数，因数×因数=积，积÷一个因数=另一个因数，被除数÷除数=商，被除数÷商=除数，商×除数=被除数）

就是不写成y=…x…的方程，x和y都在方程的一边，例如圆和椭圆的方程，直线的一般式方程。