除法的得数为什么叫商的由来
算术中除法运算的得数叫商,是由漏箭的刻度引申而来,其义来自漏箭的刻度是一个恒定的常数。
商有度量义,商量义,人与人之间的买卖关系要遵守等价交换的原则,交换双方都要度量对方货物的价值与己方货物的价值是否相当,所以,商又用为商业、商品、商人,仍为漏箭刻度的引申义。
数学中的商是什么意思
数学中的商是指一个除法运算中被除数除以除数,得到的商即为商。

商是数学中除法运算的结果。在除法中,我们将一个数(被除数)除以另一个数(除数),所得到的商代表着被除数能够被除数整除的次数。商的定义源自于数学中的除法运算,它是数学中基本的算术概念之一。
知识点运用:
商在数学中有广泛的应用。除法运算和商的概念常被用于解决实际问题、进行计算和建立数学模型。商也与其他数学概念密切相关,如分数、小数、比率等。
知识点例题讲解:
例题1:计算16除以4的商。
解答:16除以4,得到的商为4。因为4 × 4 = 16,所以16能够被4整除,商为4。
例题2:如果一个商品的价格是120元,而每件商品的售价是15元,问可以卖出多少件商品?
解答:我们可以用商来解决这个问题。将商品的价格120元除以每件商品的售价15元,即 120 ÷ 15 = 8。所以可以卖出8件商品。
延伸阅读:
商是数学中基本的概念之一,你可以进一步学习关于除法、商和相关概念的知识。可以深入了解整数除法、小数除法、分数除法等,以及商在代数学、数论、几何学等其他数学分支中的应用。你可以查阅数学教科书、在线学习资源或参考数学专业的参考书籍。
除法的得数为什么叫商
是一种数学术语。公式是:(被除数-余数)÷除数=商,记作:被除数÷除数=商··· ···余数
除法是四则运算之一。两个数相除又叫做两个数的比。
若ab=c(b≠0),用积数c和因数b来求另一个因数a的运算就是除法,写作c÷b,读作c除以b(或b除c)。其中,c叫做被除数,b叫做除数,运算的结果a叫做商。
计算方法:
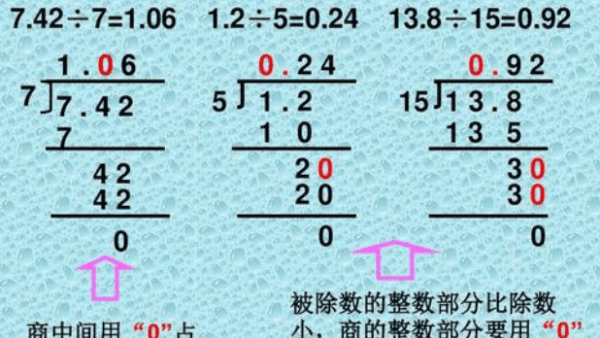
根据乘法表,两个整数可以用长除法(直式除法)笔算。 如果被除数有分数部分(或者说是小数点),计算时将小数点带下来就可以。
如果除数有小数点,将除数与被除数的小数点同时移位,直到除数没有小数点。算盘也可以做除法运算。
扩展资料性质:
被除数扩大(缩小)n倍,除数不变,商也相应的扩大(缩小)n倍。
除数扩大(缩小)n倍,被除数不变,商相应的缩小(扩大)n倍。
被除数连续除以两个除数,等于除以这两个除数之积。有时可以根据除法的性质来进行简便运算。如:300÷25÷4=300÷(25×4)除以一个数就=这个数的倒数
数学商指的是什么内容
在数学中,商指的是两个数相除得到的结果。下面是详细描述:
一、定义与概念
1.1商的定义:在数学中,商是指将一个数除以另一个数所得到的结果。
1.2商的符号表示:通常用符号“÷”或“/”表示除法运算,商用“q”表示。

二、商的特点与性质
2.1唯一性:对于任意两个数a和b(其中b不等于0),商q是唯一确定的,即a/b=q。
2.2形式记法:商可以用分数形式、小数形式或百分数形式来表示,具体形式取决于被除数和除数的类型。
2.3商的无穷性:某些除法运算可能会得到无限循环的商,这种情况下商可以用无限不循环小数表示。
三、商的计算方法
3.1整除运算:当被除数能够整除除数时,商是一个整数,没有余数。
3.2有限小数运算:当被除数不能整除除数时,商是一个有限小数,可以通过长除法或短除法等方法计算得到。
3.3无限循环小数运算:当被除数不能整除除数时,商是一个无限循环小数,可以通过长除法或观察规律等方法计算得到。

四、商的应用领域
4.1比率与比例:商在比率和比例中起到重要的作用,可以表示两个数之间的比例关系。
4.2分数运算:商可以表示分数的除法运算,如将一个数除以另一个数得到的结果。
4.3统计与概率:商在统计学和概率论中有广泛应用,可以表示事件发生的概率或频率。
五、其他相关概念
5.1商的倒数:商的倒数是指商的倒数值,即原商的倒数再取倒数。商的倒数可以用来表示乘法的逆运算。
5.2商的倍数:商的倍数是指商乘以一个整数或分数所得到的结果,表示一个数相对于另一个数的倍数关系。
5.3商的约分:当商为分数形式时,可以进行约分操作,把商表示为最简分数形式。
总结:在数学中,商指的是将一个数除以另一个数所得到的结果。商具有唯一性、形式记法和无穷性等特点和性质。商的计算方法可以通过整除运算、有限小数运算和无限循环小数运算等方式来计算。
商在比率与比例、分数运算、统计与概率等领域有广泛的应用。此外,商的倒数、商的倍数和商的约分也是与商相关的重要概念。
以上就是关于数学中的商是什么意思,除法的得数为什么叫商的由来的全部内容,以及除法的得数为什么叫商的由来的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。


