两个质数的乘积是什么
两个质数的乘积是两个质数相乘的积一定是合数,也一定是它们的最小公倍数。质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。
质数的个数是无穷的,欧几里得的《几何原本》中有一个经典的证明。它使用了证明常用的方法:反证法。
具体证明如下:假设质数只有有限的n个,从小到大依次排列为p1,p2,……,pn,设N=p1×p2×……×pn,那么,N+1是素数或者不是素数。
两个质数的乘积一定是
两个质数的乘积一定是合数。
积本身就有两个质因数。合数是指在大于1的整数中除了能被1和本身整除外,还能被其他数(0除外)整除的数。与之相对的是质数,而1既不属于质数也不属于合数,最小的合数是4。
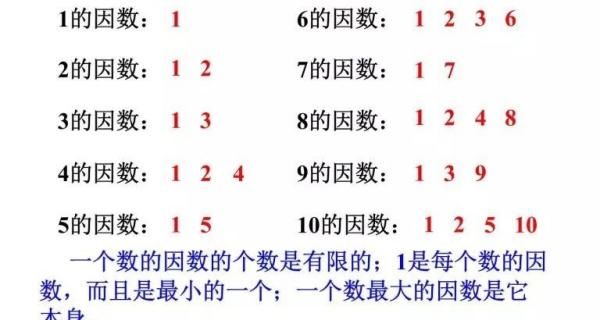
只有1和它本身两个因数的自然数,叫质数(或称素数)。

如:由2÷1=2,2÷2=1,可知2的因数只有1和它本身2这两个因数,所以2就是质数。与之相对立的是合数:“除了1和它本身两个因数外,还有其它因数的数,叫合数。”
如:4÷1=4,4÷2=2,4÷4=1,很显然,4的因数除了1和它本身4这两个因数以外,还有因数2,所以4是合数。
100以内的质数有:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97,一共有25个。
质数的个数是无穷的。欧几里得的《几何原本》中的证明使用了证明常用的方法:反证法。
具体证明如下:假设质数只有有限的n个,从小到大依次排列为p1,p2,……,pn,设N=p1×p2×……Xpn,那么,N+1是素数或者不是素数。
如果N+1为素数,则N+1要大于p1,p2,....,pn,所以它不在那些假设的素数集合中。
如果N+1为合数,因为任何一个合数都可以分解为几个素数的积;而N和N+1的最大公约数是1,所以N+1不可能被p1,p2,..,pn整除,所以该合数分解得到的素因数肯定不在假设的素数集合中。
两个质数相乘的积是 A.质数B.合数C.可能是质数也可能是合数D.无法确定
解答:解:两个质数相乘的积至少有4个因数,如:2×3=6,6的因数有:1、2、3、6,再如:3×5=15,15的因数有:1、3、5、15,所以两个质数相乘的积一定是合数.
故选:B.
两个质数的乘积是什么数
两个质数的乘积是两个质数相乘的积一定是合数,也一定是它们的最小公倍数。质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。
质数的个数是无穷的,欧几里得的《几何原本》中有一个经典的证明。它使用了证明常用的方法:反证法。
具体证明如下:假设质数只有有限的n个,从小到大依次排列为p1,p2,……,pn,设N=p1×p2×……×pn,那么,N+1是素数或者不是素数。
两个质数的积一定是什么数
两个质数的积一定是合数,例如2*2=4,4*4=16。
因为根据定义可知,一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;否则称为合数。所以两个质数的积一定是一个合数。
合数是指在大于1的整数中除了能被1和本身整除外,还能被其他数(0除外)整除的数。与之相对的是质数,而1既不属于质数也不属于合数。最小的合数是4。其中,完全数与相亲数是以它为基础的。

扩展资料
质数的性质
质数具有许多独特的性质:
(1)质数dup的约数只有两个:1和p。
(2)初等数学基本定理:任一大于1的自然数,要么本身是质数,要么可以分解为几个质数之积,且这种分解是唯一的。
(3)质数的个数是无限的。
(4)质数的个数公式 是不减函数。
(5)若n为正整数,在 到 之间至少有一个质数。
(6)若n为大于或等于2的正整数,在n到 之间至少有一个质数。
(7)所有大于10的质数中,个位数只有1,3,7,9。
以上就是关于两个质数的乘积是什么,两个质数的乘积一定是的全部内容,以及两个质数的乘积是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。