平行线有几种判定方法
1、同位角相等,两条线平行知。
2、内错角相等,两条线平行。
3、同旁内角互补,两条线平行。
4、经过直线外一点,有且只有一条直线与已知直线平行。
5、如果两条直线都与第三条直线道直线平行,那么这两条直线也互相平行。
平行线的判定定理:
(1)两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。(内错角相等,两直线平行)
(2)两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。(同旁内角互补,两直线平行)
(3)两直线都与第三条直线平行,那么这两条直线也互相平行。(若直线a平行于直线b,直线b平行于直线c,那么直线a也平行于直线c)(等量代换)。
平行线的9种判定方法
平行线的9种判定方法如下:
平行线是指:在同一平面内永不相交的两条直线。判定平行线的方法包括:同位角相等,两直线平行、内错角相等,两直线平行、同旁内角互补,两直线平行(曲线不参与)。
极简分析:
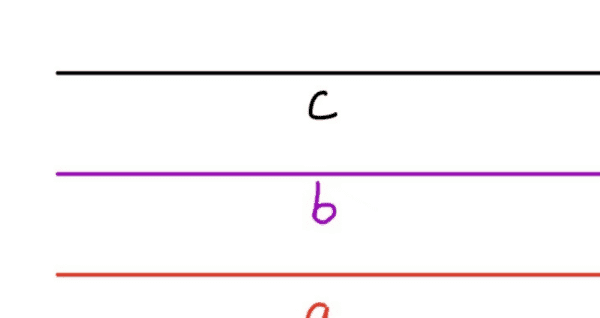
在做题的时候一定要注意,我们在得出一些结论的时候,要知道用的是性质还是判定。通过平行得到角相等/互补,是性质;通过角相等/互补得到平行,是判定。
在找角的时候,一定要清楚,是组成角的直线是哪两条直线,尤其像这种图形,非常容易判断错,所以我建议大家把角画出来,看起来就很容易了。
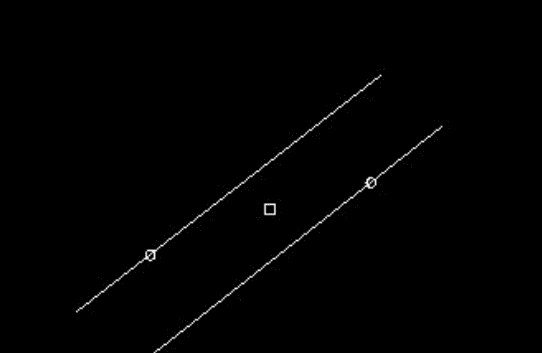
平行线的基本性质:
在同一平面内,不相交的两条直线叫做平行线。平行线一定要在同一平面内定义,不适用于立体几何,比如异面直线,不相交,也不平行。
1、经过直线外一点,能且只能画一条直线与已知直线平行。
2、两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补。
3、两条直线平行于第三条直线时,两条直线平行。
4、平行线分三角形对应边成比例。这几条命题依赖于欧氏几何的第五公设(平行公理),所以在非欧几何中不成立。
判断两条直线平行的方法有哪些
1、同位角相等两直线平行
在同一平面内,两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
2、内错角相等两直线平行
在同一平面内,两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
3、同旁内角互补两直线平行。
在同一平面内,两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。

扩展资料:
平行公理
在欧几里得的几何原本中,第五公设(又称为平行公理)是关于平行线的性质。
它的陈述是:“如果两条直线被第三条直线所截,一侧的同旁内角之和大于两个直角,那么最初的两条直线相交于这对同旁内角的另一侧。”
这条公理的陈述过于冗长。在1795年,苏格兰数学家Playfair提出了以下以下公理作为平行公理的代替,在被人们广泛的使用。
在同一平面内,过直线外一点,有且只有一条直线与这条直线互相平行。
平行公理的推论:(平行线的传递性) 如果两条直线都和第三条直线平行,那么这两条直线也互相平行。可以简称为:平行于同一条直线的两条直线互相平行
参考资料:
平行线的判定方法是什么
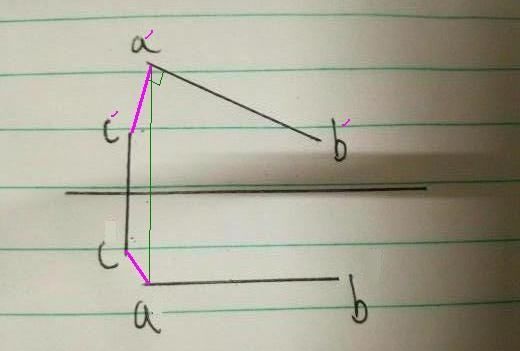
如图所示:两直线如果相交、平行或交叉的投影规律。
两直线相交:两直线的同面投影相交,且投影交点的连线垂直于对应轴;
两直线平行:两直线的同面投影平行,方向一致,且各投影长度比相等;
两直线交叉:不满足平行和相交,即是交叉位置;
工程制图判断两条直线的相对位置:
如果两条直线的投影在各投影面上都平行,就可知判断这两条直线平行。
扩展资料:
性质定理1:如果一条直线垂直于一个平面,那么该直线垂直于平面内的所有直线。
性质定理2:经过空间内一点,有且只有一条直线垂直已知平面。
性质定理3:如果在两条平行直线中,有一条直线垂直于一个平面,那么另一条直线也垂直于这个平面。
推论:空间内如果两条直线都与第三条直线平行,那么这两条直线平行。该推论意味着平行线的传递性不仅在平面几何上,在空间几何上也成立。
以上就是关于平行线的9种判定方法,平行线有几种判定方法的全部内容,以及平行线有几种判定方法的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。