f(x)函数怎么解
f(x)函数的解法有解析式法、列表法、图像法。
一、解析式法。用含有数学关系的等式来表示两个变量之间的函数关系的方法叫做解析式法。这种方法的优点是能简明、准确、清楚地表示出函数与自变量之间的数量关系;缺点是求对应值时往往要经过较复杂的运算。
二、用列表的方法来表示两个变量之间函数关系的方法叫做列表法。这种方法的优点是通过表格中已知自变量的值,可以直接读出与之对应的函数值;缺点是只能列出部分对应值。
三、把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象。这种表示函数关系的方法叫做图象法。
f(x)函数怎么解
f(x)是一个以x为自变量的函数。
给定一个数集A,假设其中的元素为x。现对A中的元素x施加对应法则f,记作f(x),得到另一数集B。假设B中的元素为y。则y与x之间的等量关系可以用y=f(x)表示。
例如:y=x,也可写成f(x)=x,意思是一样的。
f(a)=0,是说这个函数f(x)中,当x=a时,函数值为0。
函数的由来
中文数学书上使用的“函数”一词是转译词。是我国清代数学家李善兰在翻译《代数学》(1859年)一书时,把“function”译成“函数”的。
中国古代“函”字与“含”字通用,都有着“包含”的意思。李善兰给出的定义是:“凡式中含天,为天之函数。”中国古代用天、地、人、物4个字来表示4个不同的未知数或变量。这个定义的含义是:“凡是公式中含有变量x,则该式子叫做x的函数。”
所以“函数”是指公式里含有变量的意思。我们所说的方程的确切定义是指含有未知数的等式。但是方程一词在我国早期的数学专著《九章算术》中,意思指的是包含多个未知量的联立一次方程,即所说的线性方程组。
f(x)函数怎么解
定义域:直接分母不等于零就可以求出x定义域,即x^2+9 ≠ 0
函数的奇偶性:奇函数f(-x)=-f(x),偶函数f(-x)=f(x),奇函数若x=0可以取则f(0)=0
3. 这类题型建议求f(x)导函数f'(x),分式类型函数求导公式:
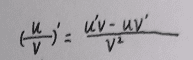
分式函数求导
4. 求得导函数如图所示:令分子等于零解得x=±3,函数导函数在[-3,3]小于等于零,在(负无穷,-3)和(3,正无穷)都大于零,所以函数在[-3,3]为单调增函数,其他区域为单调减函数,由此画出函数图像如下:
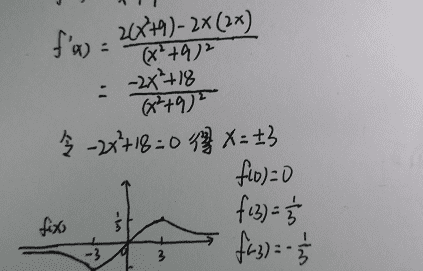
导函数
5. C选项不确定,由题意只能看出函数不是周期函数,函数只有一个零点x=0,所以f(x+2022)的零点应该会是x+2022=0,即x=-2022
6. 好久了,好多东西忘了,有问题也请指出
高中函数fx解析式的求法
直接法:
例1、在x克a%的盐水中,加入y克b%的盐水,浓度变为c%(a,b>0,a,b不相等),则x与y的函数关系是_________.
解析:由题意可得,,∴所求函数的解析式为:。
小结:此法常用于与函数有关的应用题。
待定系数法:
例2、已知f
(x)是二次函数且f(x+1)+f(x-1)=2x2-4x+4,则f
(x)=___.解:由题意可设:f(x)=ax2+bx+c,则f(x-1)+f(x+1)=a(x+1)2+b(x+1)+c+a(x-1)2+b(x-1)+c=
2ax2+2bx+2a+2c=2x2-4x+4对x∈R恒成立,从而有
。
小结:当已知函数的类型时,常用此法。
换元法:
例3、已知f
,则f(x)=____________.
解:设u=≥1,则,则=
,∴f(x).
4、凑配法:如例4(同例3)解:∵f
=,∴f(x)。
小结:当已知函数的一个复合函数的解析式时,常用换元法或凑配法。
5、方程组法:如例5、已知f(x)+2,求f(x).
解:∵①∴
以代替①式中x的得②
∴①-②2得:,即。
小结:当已知x与或x与-x的函数值的一个方程时,可考虑用此法。
6、相关点法:如例6、已知函数f(x)=2x+1与函数y=g(x)的图象关于直线x=2成轴对称图形,试求函数y=g(x)的解析式。
解:设在所求函数的图象上,点是M关于直线x=2的对称点,则
又∴即g(x)=9-2x.
小结:当以函数图象的对称性为已知条件时,可考虑用此法。
7、叠加法:如例7、已知函数f(x)对任意的x,y都有f(x+y)=f(x)+f(y)+(x+y)+1,且f(1)=1,若x∈N,试求f(x)的解析式。
解:令x=y=0,则有f(0)=f(0)+f(0)+0,∴f(0)=0,再令y=1,则f(x+1)=f(x)+f(1)+x,
①,令①中x=1,2,3,…,n-1,得f(2)=f(1)+2,f(3)=f(2)+3,
f(4)=f(3)+4,…,f(n-1)=f(n-2)+(n-1),f(n)=f(n-1)+n,以上各式左右两边分别相加得:
f(n)=f(1)+2+3+…+n=1+2+3+…+(n-1)=,当n=0时,f(0)=0成立。
故f(x)的表达式为f(x)=,x∈N.
小结:此法只适用于定义域为整数集(或它的子集)的函数,关键是可求得f(n)-f(n-1).
去百度文库收索吧,总结得很好呢!
以上就是关于fx函数怎么解的全部内容,以及f(x)函数怎么解的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。




