帕斯卡定理是什么
1、帕斯卡定理指圆锥曲线内接六边形(包括退化的六边形)其三对边的交点共线,与布列安桑定理对偶,是帕普斯定理的推广。定理约于公元1639年为法国数学家布莱士·帕斯卡(BlaisePascal)所发现,被称为帕斯卡定理,是射影几何中的一个重要定理。
2、如果一个六边形内接于一条二次曲线(圆、椭圆、双曲线、抛物线),那么它的三对对边的交点在同一条直线上。由于六边形的存在多种情况,帕斯卡定理的图形也存在多种,它们虽然看起来截然不同,但均为帕斯卡定理,证明它们的方法也是相同的
帕斯卡定理数学
帕斯卡定理,是二次曲线上的定理。同样适应于相交的直线,圆锥曲线。为射影几何的重要定理。
射影几何的定理,单纯用综合几何证明会比较困难。尤其是圆锥曲线上的射影几何定理。
相交直线上的帕斯卡定理就是帕普斯定理,前文已证。
下面只证圆上的帕斯卡定理。根据射影几何的不变量,可知,在圆上成立,在其它圆锥曲线上也成立。
设ABCDEF为圆的内接六边形,AE与BF交于点P,BD与CE交于点Q,AD与CF交于点T,则P,T,Q三点共线。
证明:作三角形TCD的外接圆,交EC,BD于点G和点H。
连接BE。连接GT,TH,HG。
在TCD的外接圆中,和原来的圆中,由圆周角定理,得,角TGC=角TDC=角ADC=角AEC,即角TGC=角AEC,因此,PE//TG。
同理可证,EB//GH,PB//TH。
三角形PEB与三角形TGH位似。PT连线过位似中心Q。
所以P,T,Q三点共线。
(这个证明的辅助线作法可遇而不可求。如果真的需要用到帕斯卡定理来证明的题目,那么,多半是数学竞赛才有的题。)
射影几何用交比来证明此定理。
什么叫帕斯卡定律
帕斯卡定理
指圆锥曲线内接六边形其三对边的交点共线,与布列安桑定理对偶,是帕普斯定理的推广。该定理由法国数学家布莱士·帕斯卡提出,是射影几何中的一个重要定理。
特殊情况的证明:
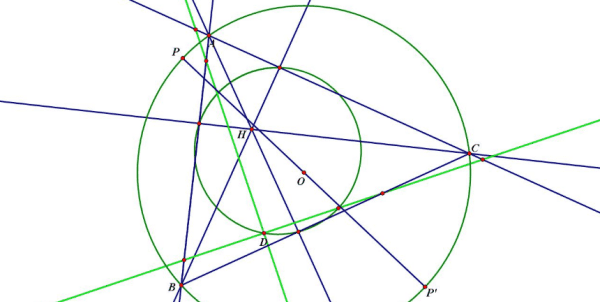
如图,圆锥曲线是一圆,圆内接六边形ABCDEF的边AB、DE的延长线交于点G,边BC、EF的延长线交于点H,边CD、FA的延长线交于点K。
延长AB、CD、EF,分别交直线CD、EF、AB于M、N、L三点,构成△LMN。
直线BC截LM、MN、NL于B、C、H三点,则
…①
直线DE截LM、MN、NL于G、D、E三点,则
…②
直线AF截LM、MN、NL于A、K、F三点,则
…③
连BE,则LA·LB=LF·LE,
∴
…④。
同理
…⑤,
…⑥。
将①②③④⑤⑥相乘,得
。
∵点H、G、K在△LMN的边LN、LM、MN的延长线上,
∴H、G、K三点共线。
帕斯卡定理是什么意思
1、帕斯卡定理指圆锥曲线内接六边形(包括退化的六边形)其三对边的交点共线,与布列安桑定理对偶,是帕普斯定理的推广。定理约于公元1639年为法国数学家布莱士·帕斯卡(BlaisePascal)所发现,被称为帕斯卡定理,是射影几何中的一个重要定理。
2、如果一个六边形内接于一条二次曲线(圆、椭圆、双曲线、抛物线),那么它的三对对边的交点在同一条直线上。由于六边形的存在多种情况,帕斯卡定理的图形也存在多种,它们虽然看起来截然不同,但均为帕斯卡定理,证明它们的方法也是相同的
什么是帕斯卡定理?影响液压泵效率的因素有哪些?
(Pascal law)
帕斯卡定律是流体(气体或液体)力学中,由于液体的流动性,封闭容器中的静止流体的某一部分发生的压强变化,将毫无损失地传递至流体的各个部分和容器壁。帕斯卡首先阐述了此定律。压强等于作用力除以作用面积。根据帕斯卡定律,在水力系统中的一个活塞上施加一定的压强,必将在另一个活塞上产生相同的压强增量。如果第二个活塞的面积是第一个活塞的面积的10倍,那么作用于第二个活塞上的力将增大为第一个活塞的10倍,而两个活塞上的压强仍然相等。
这一定律是法国物理学家帕斯卡首先提出的。这个定律在生产技术中有很重要的应用,液压机就是帕斯卡原理的实例。它具有多种用途,如液压制动等。帕斯卡还发现:静止流体中任一点的压强各向相等,即该点在通过它的所有平面上的压强都相等。这一事实也称作帕斯卡原理.
以上就是关于帕斯卡定理数学,帕斯卡定理是什么的全部内容,以及帕斯卡定理是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。