a⊕b⊕c怎么化简
a⊕b⊕c化简方式:F=A⊕B=A“B+AB“F“=(A⊕B)“=(A“B+AB“)“=(A+B“)(A“+B)=AB+A“B“=A⊙B可期待:Y“=A⊙B⊙C。
异或是一个数学运算符。它应用于逻辑运算。异或的数学符号为“⊕”,其运算法则为:a⊕b=(?a∧b)∨(a∧?b)。如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0。
a异或b异或c的反函数等于什么
Y = A⊕B⊕C
Y' = ( A⊕B⊕C)' ----- 这就是Y的反函数,依照定义可一步一步作下去!
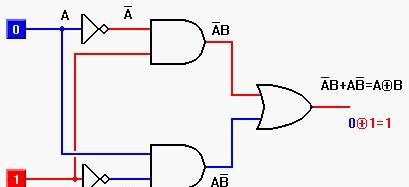
F = A⊕B = A'B+AB'
F' = (A⊕B)' = (A'B+AB')' = (A+B')(A'+B) = AB+A'B' = A⊙B
可期待:
Y' = A⊙B⊙C
但须证明!
逻辑同或运算怎么算
逻辑运算a⊕b⊕c = aVbVc
a同或b同或c =a∧b V b∧c
a⊕b同或c = (a V b)Vc
扩展资料
1、四则混合运算顺序:同级运算时,从左到右依次计算;两级运算时,先算乘除,后算加减。
有括号时,先算括号里面的,再算括号外面的;有多层括号时,先算小括号里的,再算中括号里面的,再算大括号里面的,最后算括号外面的。
2、乘法是加法的简便运算,除法是减法的简便运算。减法与加法互为逆运算,除法与乘法互为逆运算。
几个加数相加,可以任意交换加数的位置;或者先把几个加数相加再和其他的加数相加,它们的和不变。
一个数减去两个数的和,等于从这个数中依次减去和里的每一个加数。
逻辑函数a异或(a异或b)
Y = A⊕B⊕C。
Y' = ( A⊕B⊕C)' ----- 这就是Y的反函数,依照定义可一步一步作下去!
布尔代数法:按一定逻辑规律进行运算的代数。与普通代数不同,布尔代数中的变量是二元值的逻辑变量。
真值表法:采用一种表格来表示逻辑函数的运算关系,其中输入部分列出输入逻辑变量的所有可能组合,输出部分给出相应的输出逻辑变量值。
扩展资料:
计算机语言表示法:AND。
在所有参数的逻辑值为真时返回TRUE(真);只要有一个参数的逻辑值为假,则返回FALSE(假)。
语法表示为:AND(Logical1,logical2,…)。参数Logical1,logical2,…为待检验的1~30个逻辑表达式,它们的结论或为TRUE(真)或为FALSE(假)。
参数必须是逻辑值或者包含逻辑值的数组或引用,如果数组或引用内含有文字或空白单元格,则忽略它的值。如果指定的单元格区域内包括非逻辑值,AND将返回错误值“#VALUE!”。
逻辑函数a异或(a异或b)
Y = A⊕B⊕C。
Y' = ( A⊕B⊕C)' ----- 这就是Y的反函数,依照定义可一步一步作下去!
F = A⊕B = A'B+AB'。
F' = (A⊕B)' = (A'B+AB')' = (A+B')(A'+B) = AB+A'B' = A⊙B。
其中x是自变量,函数的定义域是(0,+∞),即x>0。它实际上就是指数函数的反函数,可表示为x=ay。因此指数函数里对于a的规定,同样适用于对数函数。
扩展资料:
性质:
一般地,如果a(a>0,且a≠1)的b次幂等于N,那么数b叫做以a为底N的对数,记作logaN=b,其中a叫做对数的底数,N叫做真数。
底数则要>0且≠1 真数>0,并且,在比较两个函数值时:
如果底数一样,真数越大,函数值越大。(a>1时)
如果底数一样,真数越小,函数值越大。(0
以上就是关于a⊕b⊕c怎么化简,a异或b异或c的反函数等于什么的全部内容,以及a⊕b⊕c怎么化简的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。