什么相等两直线平行
两条直线平行简单的判定方法:
(1)同位角相等,两直线平行。
(2)内错角相等,两直线平行。
(3)同旁内角互补,两直线平行。
(4)在同一平面内,两直线不相交,即平行、重合。
(5)两条直线平行于一条直线,则三条不重合的直线互相平行。
在平面上两条直线、空间的两个平面以及空间的一条直线与一平面之间没有任何公共点时,称它们平行。直线AB平行于直线CD,记作AB∥CD。平行线在无论多远都不相交。
如何判定两条直线平行的定义
1.同位角相等,两条线平行。
2.内错角相等,两条线平行。
3.同旁内角互补,两条线平行。
4.经过直线外一点,有且只有一条直线与已知直线平行。
5.如果两条直线都与第三条直线直线平行,那么这两条直线也互相平行。
平行线的判定定理:
(1)两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。(内错角相等,两直线平行)
(2)两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。(同旁内角互补,两直线平行)
(3)两直线都与第三条直线平行,那么这两条直线也互相平行。(若直线a平行于直线b,直线b平行于直线c,那么直线a也平行于直线c)(等量代换)。

扩展资料:
基本特征
平行线的定义包括三个基本特征:一是在同一平面内,二是两条直线,三是不相交。
在同一平面内,两条直线的位置关系只有两种:平行和相交。
平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。平行公理的推论体现了平行线的传递性,它可以作为以后推理的依据。
参考资料:
判断两条直线平行的方法有哪些?
1、同位角相等两直线平行
在同一平面内,两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
2、内错角相等两直线平行
在同一平面内,两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
3、同旁内角互补两直线平行。
在同一平面内,两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。

扩展资料:
平行公理
在欧几里得的几何原本中,第五公设(又称为平行公理)是关于平行线的性质。
它的陈述是:“如果两条直线被第三条直线所截,一侧的同旁内角之和大于两个直角,那么最初的两条直线相交于这对同旁内角的另一侧。”
这条公理的陈述过于冗长。在1795年,苏格兰数学家Playfair提出了以下以下公理作为平行公理的代替,在被人们广泛的使用。
在同一平面内,过直线外一点,有且只有一条直线与这条直线互相平行。
平行公理的推论:(平行线的传递性) 如果两条直线都和第三条直线平行,那么这两条直线也互相平行。可以简称为:平行于同一条直线的两条直线互相平行
参考资料:
两直线平行什么角相等
两直线平行,同位角相等,内错角相等。
同旁内角互补,这个是判定两直线平行的方法。
同位角相等或者内错角相等或者同旁内角互补,就可以判定两条直线平行。
两条直线平行的判定条件是什么意思
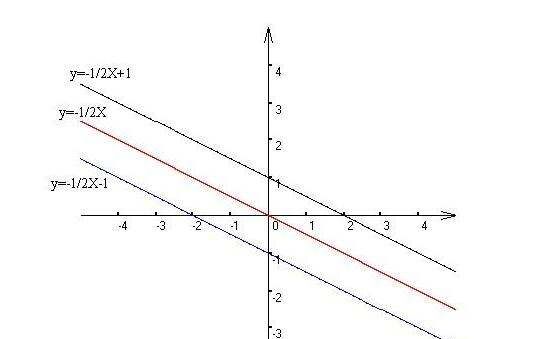
平行的直线中的函数解析式的k相等,如:y=2x+3和y=2x-1平行,斜率相等,永不相交。
两条直线平行有三个判定条件:
(1)两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。简称为:同位角相等,两直线平行。
(2)两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。简称为:内错角相等,两直线平行。
(3)两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。简称为:同旁内角互补,两直线平行。
扩展资料
运用一次函数解决实际问题
建立数学模型运用一次函数解决实际问题的一般步骤
(1)通过实验,测量获得数量足够多的两个变量的对应值。
(2)建立合适的直角坐标系,在坐标系中,以各对应值为坐标描点,并画出函数图象。
(3)观察图象特征,判定函数类型。
(4)运用得到的经验公式,进一步求得所需要的结果。
以上就是关于什么相等两直线平行,如何判定两条直线平行的定义的全部内容,以及什么相等两直线平行的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。