柱面方程怎么求
柱面方程,即母线平行于坐标轴的,将两曲面方程联立,消去母线所平行的坐标轴的字母所得即为柱面方程。柱面是直线沿着一条定曲线平行移动所形成的曲面,即动直线沿着一条定曲线平行移动所形成的曲面,动直线称为柱面的直母线,定曲线称为柱面的准线。当准线是圆时所得柱面称为圆柱面。
当准线是圆时所得柱面称为圆柱面;特别地,如果直母线垂直于圆所在平面时,所得柱面称为直圆柱面(或正圆柱面),直圆柱面也可以看成是动直线平行于定直线且与定直线保持定距离平行移动产生的,定直线是它的轴,定距离是它的半径。分别以平面上的椭圆、双曲线和抛物线为准线的柱面,称为椭圆柱面、双曲柱面和抛物柱面。它们的方程都是二次的,统称为二次柱面。在空间直角坐标系中,只含两个变量的二次方程一般总表示一个二次柱面或者两个平面。
柱面方程的形式
对空间坐标系中F(x,y)=0;
G(y,z)=0;
H(x,z)=0。这些都是柱面方程。如:x²+y²=1,就是圆柱面方程。
柱面方程表达式推导过程
柱面方程的一般表达式为:x²+y²=1;y=x²; x²/a²-y²/b²=1;x²/ a²+y² /b²=1等。
1、柱面方程表达式:对空间坐标系中F(x, y)=0;G(y,z)=0;H(x,z)=0,这些都是柱面方程。如:x²+y²=1,就是圆柱面方程表达式。
2、抛物柱面表达式:y=x²。双曲柱面表达式: x²/a²-y²/b²=1。椭圆柱面表达式:x²/ a²+y² /b²=1。
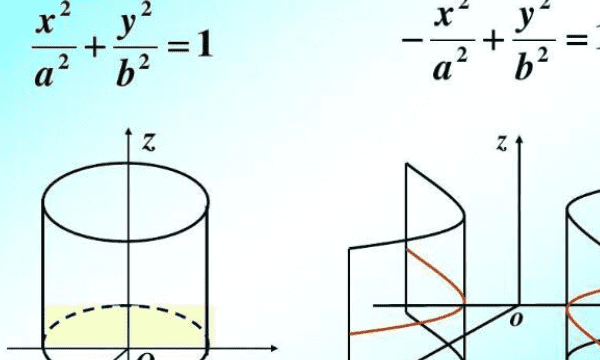
3、柱面按照其几何特性可以分为以下3种不同类型的柱面:普通柱面、直圆柱面和二次柱面。
普通柱面:若一动直线沿已知曲线C移动,且始终与某一定直线平行,则这样形成的曲面称为柱面,此时,把曲线C称为准线,动直线L称为母线。
F(x,y)=0 表示母线平行于z轴的柱面。
F(y,z)=0 表示母线平行于x轴的柱面。
F(x,z)=0 表示母线平行于y轴的柱面。

直圆柱面:如果直母线垂直于圆所在平面时,所得柱面称为直圆柱面(或正圆柱面),直圆柱面也可以看成是动直线平行于定直线且与定直线保持定距离平行移动产生的,定直线是它的轴,定距离是它的半径。
二次柱面:分别以平面上的椭圆、双曲线和抛物线为准线的柱面,称为椭圆柱面、双曲柱面和抛物柱面。它们的方程都是二次的,统称为二次柱面。在空间直角坐标系中,只含两个变量的二次方程一般总表示一个二次柱面或者两个平面。
双曲柱面的方程
消去x,就得到母线平行于x轴的柱面方程:
3y^2-z^2=16
消去y,就得到母线平行于y轴的柱面方程:
3x^2+2z^2=16
已知母线方向向量和准线求柱面方程
计算公式是:
若准线方程是f(x,y)=0,z=0,当母线的方向向量是S={L,m,n}时,柱面方程为f(x-L/n·z,y-m/n·z)=0
题中f(x,y)=y^2-4x=0,S=(2,1,-1),所以柱面方程是(y+z)^2-4(x+2z)=0
以上就是关于柱面方程怎么,柱面方程的形式的全部内容,以及柱面方程怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。