同底数幂的除法法则是什么
同底数幂的除法法则是同底数幂相除,底数不变,指数相减,同底数幂是指底数相同的幂,同底数幂之间共有5条计算性质,且对正指数幂和负指数幂均适用。
同底数幂除了除法法则,还包括有乘法法则,指的是同底数幂相乘,底数不变,指数相加,注意如不是同底数,应先变成同底数,注意符号。
分数相除的运算法则是什么
同底数幂相除的法则:同底数幂相除,底数不变,指数相减。
1、只有底数相同,才能运用此法则。
2、底数a可以是数字、字母,也可以是单项式或多项式。
3、当相除两个幂底数不同时,应想法将其化为同底数再相除。
4、条件m>n是为了保证m-n为正整数,因为目前只学了正整数指数幂;条件a≠0是保证除式有意义。
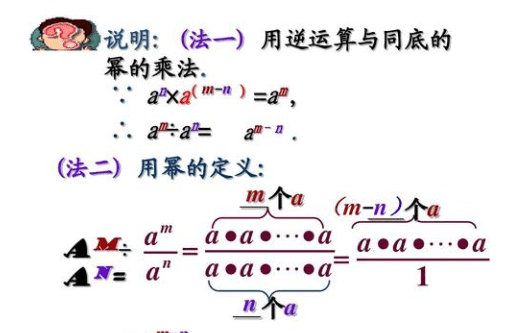
同底数幂的除法举例:
已知a、b、c表示负数,m、n、k都表示自然数,怎样决定a^m÷b^n×c^k是正数还是负数?
m、n、k都为0时,a^m÷b^n×c^k是正数
m、n、k都为偶数时,a^m÷b^n×c^k是正数
m、n、k都为奇数时,a^m÷b^n×c^k是负数
m、n、k中有一数为0,其余两数为偶数时a^m÷b^n×c^k是正数
m、n、k中有一数为0,其余两数为奇数时a^m÷b^n×c^k是正数
m、n、k中有一数为0,其余两数为一奇一偶时a^m÷b^n×c^k是负数
m、n、k中有一数为偶数,其余两数为奇数时a^m÷b^n×c^k是正数
m、n、k中有一数为奇数,其余两数为偶数时a^m÷b^n×c^k是负数
同底数幂的除法教案
任何数的零次方都等于1。题目解答如下:
a的3次方÷a的3次方=a的(3-3)次方=1
同底数幂相除,底数不变,指数相减: a^m÷a^n=a^(m-n)(m、n都是整数且a≠0)。
如a^5÷a^2=a^(5-2)=a^3 ,说明:a^m是a的m次方,a^n是a的n次方,a^(m+n)是a的m+n 次方。
扩展资料
1、计算比较法
先通过幂的计算,然后根据结果的大小,来进行比较的。
2、底数比较法
在指数相同的情况下,通过比较底数的大小,来确定两个幂的大小。
3、指数比较法
在底数相同的情况下,通过比较指数的大小,来确定两个幂的大小。
4、求差比较法
将两个幂相减,根据其差与0的比较情况,来确定两个幂的大小。
5、求商比较法
将两个幂相除,然后通过商与1的大小关系,比较两个幂的大小。
6、乘方比较法
将两个幂乘方后化为同指数幂,通过进行比较结果,来确定两个幂的大小。
7、定值比较法
通过选一个与两个幂中一个幂相接近的幂作定值,然后用两个幂与所选取的定值相比较,由此来确定两个幂的大小。
同底数幂的运算法则
1、同底数幂的乘法:
aᵐ·aⁿ·aᵖ=aᵐ⁺ⁿ⁺ᵖ(m, n, p都是正整数)。
2、幂的乘方(aᵐ)ⁿ=a(ᵐⁿ),与积的乘方(ab)ⁿ=aⁿbⁿ
3、同底数幂的除法:
(1)同底数幂的除法:aᵐ÷aⁿ=a(ᵐ⁻ⁿ) (a≠0, m, n均为正整数,并且m>n)
(2)零指数:a⁰=1 (a≠0);
(3)负整数指数幂:a⁻ᵖ= (a≠0, p是正整数),当a=0时没有意义,0⁻²,0⁻²都无意义。

扩展资料
运算规则
同底数幂相乘,底数不变,指数相加;同底数幂相除,底数不变,指数相减;幂的乘方,底数不变,指数相乘;同指数幂相乘,指数不变,底数相乘;同指数幂相除,指数不变,底数相除。
1、零指数幂
当底数n≠0时,由于nᵃ÷nᵃ=1,根据幂的运算规则可知,nᵃ÷nᵃ=nᵃ⁻ᵃ=n⁰=1,
因此定义零指数幂如下:a⁰=1,a≠0。
2、分数指数幂
设

其中n为正整数。两边同时作乘方运算,自乘n次,并根据幂的乘方的运算法则,我们可以得到以下关系式:
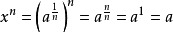
3、负指数幂
当底数n≠0时,由于n⁰÷nᵃ=1÷nᵃ=1/nᵃ,根据幂的运算规则可知,n⁰÷nᵃ=n⁰⁻ᵃ=n⁻ᵃ=1/nᵃ
因此定义负指数幂如下:a⁻ᵖ=1/aᵖ,a≠0。
以上就是关于同底数幂的除法法则是什么,分数相除的运算法则是什么的全部内容,以及同底数幂的除法法则是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。


