二次函数的对称轴公式是什么
首先确定一般式以确定a,b,c的值,一般式为y=ax^2+bx+c,对称轴公式为x=-b/2a,如果是顶点式y=a(x-h)^2+k,则对称轴x=h。
二次函数(quadraticfunction)是一个二次多项式(或单项式),它的基本表示形式为y=ax?+bx+c(a≠0)。二次函数最高次必须为二次,二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。
二次函数对称轴公式是什么?
x=-b/2a
二次函数对称轴公式是x=-b/2a。二次函数的基本表示形式为y=a(x的平方)+bx+c(a不等于0)。二次函数最高次必须为二次,二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。
二次函数表达式为y=a(x的平方)+bx+c(a不等于0),它的定义是一个二次多项式(或单项式)。如果令y值等于零,则可得一个二次方程。该方程的解称为方程的根或函数的零点。二次函数对称轴公式是x=-b/2a。二次函数最高次必须为二次,二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。
变量不同于未知数,不能说二次函数是指未知数的最高次数为二次的多项式函数。未知数只是一个数(具体值未知,但是只取一个值),变量可在一定范围内任意取值。在方程中适用未知数的概念(函数方程、微分方程中是未知函数,但不论是未知数还是未知函数,一般都表示一个数或函数也会遇到特殊情况),但是函数中的字母表示的是变量,意义已经有所不同。从函数的定义也可看出二者的差别。
三种表达式:
一般式:y=ax²+bx+c(a,b,c为常数,a≠0)
顶点式:y=a(x-h)²+k[抛物线的顶点P(h, k)]
交点式:y=a(x-x1)(x-x2)[仅限于与x轴有交点A(x1,0)和B(x2,0)的抛物线]
二次函数对称轴公式是什么?
二次函数对称轴公式:x=-b/2a。二次函数的基本表示形式为y=a(x的平方)+bx+c(a不等于0)。二次函数最高次必须为二次,二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。
二次函数表达式为y=a(x的平方)+bx+c(a不等于0),它的定义是一个二次多项式(或单项式)。
如果令y值等于零,则可得一个二次方程。该方程的解称为方程的根或函数的零点。
二次函数的历史:
大约在公元前480年,古巴比伦人和中国人已经使用配方法求得了二次方程的正根,但是并没有提出通用的求解方法。公元前300年左右,欧几里得提出了一种更抽象的几何方法求解二次方程。
7世纪印度的婆罗摩笈多是第一位懂得用使用代数方程的人,它同时容许有正负数的根。
11世纪阿拉伯的花拉子密 独立地发展了一套公式以求方程的正数解。亚伯拉罕巴希亚(亦以拉丁文名字萨瓦索达著称)在他的著作Liber embadorum中,首次将完整的一元二次方程解法传入欧洲。
据说施里德哈勒是最早给出二次方程的普适解法的数学家之一。但这一点在他的时代存在着争议。这个求解规则是:在方程的两边同时乘以二次项未知数的系数的四倍;在方程的两边同时加上一次项未知数的系数的平方;然后在方程的两边同时开二次方(引自婆什迦罗第二)
2次函数对称轴公式a值怎么算出来
2次函数对称轴公式介绍如下:
抛物线对称轴公式是x=-b/2a。
说明:
垂直于准线并通过焦点的线(即通过中间分解抛物线的线)被称为“对称轴”。y=ax²+bx+c=a(x²+b/ax)+c=a(x²+b/ax+b²/4a²)+c-b²/4a=a(x+b/2a)²-(-4ac+b²)/(4a)顶点(-b/2a,(4ac-b²)/4a)。
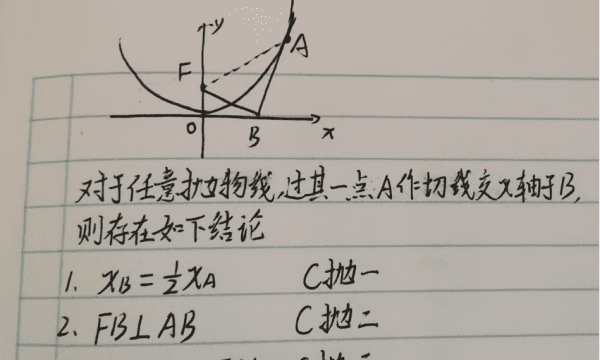
理解:
当二次函数形式为y=ax^2+c(a≠0)时二次函数对称轴是y轴,用公式表示就是x=0,而顶点式y=a(x-h)^2+k可以理解为上述形式的二次函数平移后h个单位后的结果,也就是说对称轴从y轴平移了h个单位。用公式表示就是x=h。
抛物线概念:
在数学中,抛物线是一个平面曲线,它是镜像对称的,并且当定向大致为U形(如果不同的方向,它仍然是抛物线)。它适用于几个表面上不同的数学描述中的任何一个,这些描述都可以被证明是完全相同的曲线。
抛物线的一个描述涉及一个点(焦点)和一条线(准线)。焦点并不在准线上。抛物线是该平面中与准线和焦点等距的点的轨迹。
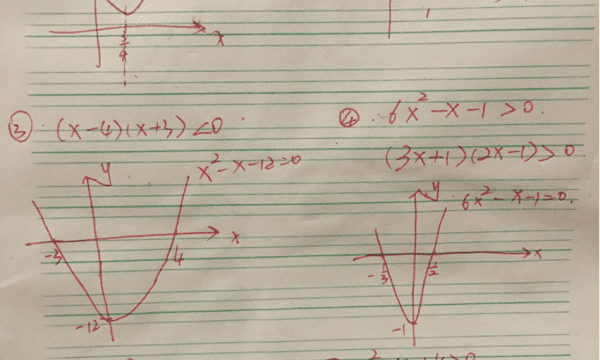
抛物线的几何性质:
1、有关切线、法线的几何性质
设抛物线上一点P的切线与准线相交于Q,F是抛物线的焦点,则PF⊥QF。且过P作PA垂直于准线,垂足为A,那么PQ平分∠APF。
过抛物线上一点P作准线的垂线PA,则∠APF的平分线与抛物线切于P。为性质(1)第二部分的逆定理从这条性质可以得出过抛物线上一点P作抛物线的切线的尺规作图方法。
2、有关弦的几何性质
焦点弦两端的切线互相垂直,并且垂足在准线上。过焦点弦的端点A、B作准线的垂线,垂足分别为M、N。设A、B处的切线相交于P,则P是MN中点,并且以AB为直径的圆切准线于P。
若抛物线的两条焦点弦相等,连接这两条焦点弦的中点,则连线与轴垂直。抛物线的一条弦AB与轴相交于P(不一定是焦点F),过A、B分别作轴的垂线AM、BN,抛物线顶点为O,则OP²=AM*BN。
以上就是关于二次函数对称轴公式是什么,二次函数的对称轴公式是什么的全部内容,以及二次函数的对称轴公式是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。