6大基本初等函数有哪些
6大基本初等函数有常数函数,幂函数,指数函数,对数函数,三角函数以及反三角函数。
函数,最早由中国清朝数学家李善兰翻译,出于其著作《代数学》。
之所以这么翻译,他给出的原因是“凡此变数中函彼变数者,则此为彼之函数”,也即函数指一个量随着另一个量的变化而变化,或者说一个量中包含另一个量。
哪些基本初等函数是有界函数
主要有以下 6 个 :
反正弦函数:y = arcsin x
使用几何画板绘制的三角函数图像
反余弦函数:y = arccos x
反正切函数:y = arctan x
反余切函数:y = arccot x
反正割函数:y = arcsec x
反余割函数:y = arccsc x
六大基本初等函数
六大基本初等函数:
常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数。
一、常数函数
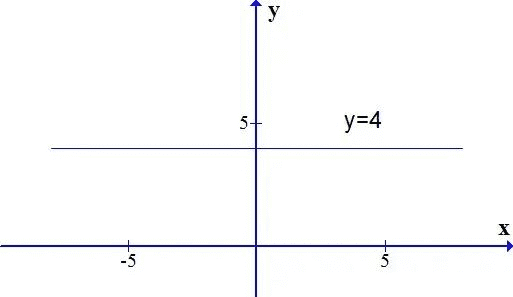
常数函数是指函数值不发生改变的函数,例如 y=f(x)=4 ,无论 x 取何值,函数值都是 4,如图
二、幂函数
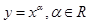
幂函数的形式
常见的幂函数有以下5个
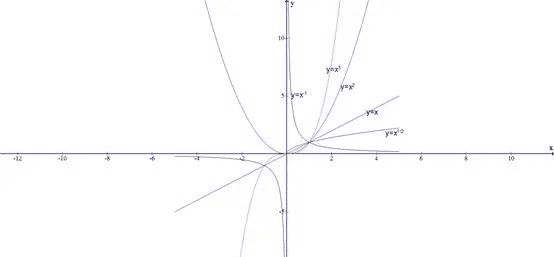
三、指数函数
四、对数函数
五、三角函数
三角函数一共有6个,y=sinx ,y=cosx, y=tanx ,y=cotx, y=secx, y=cscx
有一些重要的三角函数公式
1.平方关系
2.商的关系
3.倒数关系
4.半角公式(降幂公式)
六、反三角函数
反三角函数有四个:y=arcsinx ,y=arccosx, y=arctanx ,y=arccotx.
要注意:三角函数有6个,但是反三角函数只有4个。
基本初等函数包括什么函数
高等数学将基本初等函数归为五类:幂函数、指数函数、对数函数、三角函数、反三角函数。数学分析将基本初等函数归为六类:幂函数、指数函数、对数函数、三角函数、反三角函数、常数函数。
扩展资料:
基本初等函数的函数性质:
一、幂函数
幂函数的图象一定会出现在第一象限内,一定不会出现在第四象限,至于是否出现在第二、三象限内,要看函数的奇偶性;幂函数的图象最多只能同时出现在两个象限内;如果幂函数图象与坐标轴相交,则交点一定是原点。
二、指数函数
当a>1时,指数函数对于x的负数值非常平坦,对于x的正数值迅速攀升,在 x等于0的时候,y等于1。当0
三、对数函数
定义域求解:对数函数的定义域是{x 丨x>0},但如果遇到对数型复合函数的定义域的求解,除了要注意大于0以外。
还应注意底数大于0且不等于1,如求函数y=logx(2x-1)的定义域,需同时满足x>0且x≠1和2x-1>0 ,得到x>1/2且x≠1,即其定义域为 {x 丨x>1/2且x≠1}。
四、三角函数
三角函数通常定义为包含这个角的直角三角形的两个边的比率,也可以等价的定义为单位圆上的各种线段的长度。更现代的定义把它们表达为无穷级数或特定微分方程的解,允许它们扩展到任意正数和负数值,甚至是复数值。
五、反三角函数
三角函数的反函数不是单值函数,因为它并不满足一个自变量对应一个函数值的要求,其图像与其原函数关于函数y=x对称。欧拉提出反三角函数的概念,并且首先使用了“arc+函数名”的形式表示反三角函数。
六、常数函数
f: A→B是一个常数函数。 对所有函数g, h: C→A, fog=foh(“o”表示复合函数)。 f与其他任何函数的复合仍是一个常数函数。 上面所给的常数函数的第一个描述,是范畴论中常数态射更多一般概念的激发和定义的性质。
6类基本初等函数有哪些
6大基本初等函数有常数函数,幂函数,指数函数,对数函数,三角函数以及反三角函数。函数,最早由中国清朝数学家李善兰翻译,出于其著作《代数学》。之所以这么翻译,他给出的原因是“凡此变数中函彼变数者,则此为彼之函数”,也即函数指一个量随着另一个量的变化而变化,或者说一个量中包含另一个量。
以上就是关于6大基本初等函数有哪些,哪些基本初等函数是有界函数的全部内容,以及6大基本初等函数有哪些的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。