任何数的0次幂是多少
任何除0以外的数的0次幂是1,同底数幂的乘法,即同底数幂相乘,底数不变,指数相加。
同底数幂的除法,即同底数幂相除,底数不变,指数相减。
幂的乘方,底数不变,指数相乘。
商的乘方即分式乘方,分子分母分别乘方,指数不变?。
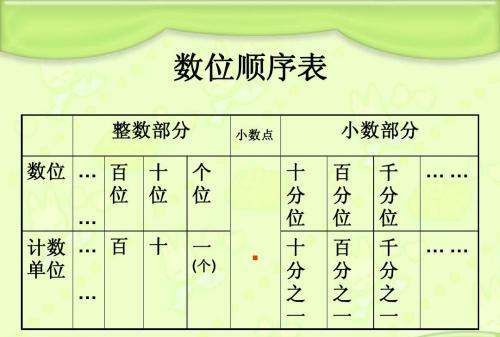
指数是幂运算a?(a≠0)中的一个参数,a为底数,n为指数,指数位于底数的右上角。
任何数的0次幂都等于1
任何数的0次幂如下:
任何数的0次幂,通常表示为a^0,是一个数学概念,指的是任意非零实数a的0次方。在数学中,任何非零数的0次幂定义为1。
任何数的0次幂的介绍:
在数学中,一个数的幂表示这个数连乘若干次的结果。通常情况下,一个数的幂是指这个数连乘自身若干次。例如,2的3次幂表示2自乘3次,即2×2×2=8。然而,当指数为0时,任何非零数的0次幂定义为1。

这个定义可以通过以下推理进行解释:假设我们有一个非零数a,并将其的n次幂记为a^n。当n>0时,我们可以将a^n定义为a自乘n次的结果。现在,如果我们考虑n=0的情况,那么根据此定义,a^0应该是什么呢?为了保持数学的一致性和运算法则的相容性,我们将其定义为1。
通过这个定义,任何非零数的0次幂都等于1。例如,2^0=1,3^0=1,5^0=1,以及任何其他非零数的0次幂都等于1。
相关扩展:
零的0次幂:
与任何非零数的0次幂不同,零的0次幂是一个未定义的表达式。这是因为零没有明确的倒数或反操作。在数学中,我们无法将零的0次幂定义为1。因此,0^0是一个有争议和不确定的表达式,在不同的数学分支和问题中可能会有不同的处理方式。
幂的运算法则:
幂具有一些运算法则,可以用于简化计算和推导等。其中一些法则也适用于0次幂。例如,对于任意非零数a,我们有a^m×a^n=a^(m+n)。根据这个法则,我们可以得出结论,对于非零数a,a^0×a^0=a^(0+0)=a^0,进一步推导即可得到a^0=1。
零次幂的应用:
虽然零次幂在数学上可能没有明确的定义,但它在某些数学和物理问题中可以有实际的应用。例如,它在排列组合、二项式定理、级数展开和概率论等领域中被广泛使用。在这些应用中,通常通过定义特殊情况来处理零次幂的问题,以使得相应的表达式在数学运算中具有一致性和可计算性。
幂函数的图像:
幂函数是指以自然对数为底的指数函数。当幂函数的底大于1时,幂函数呈现递增的趋势;而当底小于1时,幂函数呈现递减的趋势。当底为1时,幂函数的值始终为1,不管指数如何变化。这可以被视为0次幂的图像特征,在指数为0时,函数值保持不变为1。
总结:
任何非零数的0次幂被定义为1。这个定义保持了幂运算的运算法则和数学一致性。尽管0次幂在零的情况下是未定义的,并且可能引发争议,但在许多数学和物理问题中,它仍然具有实际的应用和推导价值。
任何数的零次方是多少
任何数的零次方是1,相关内容如下:

1.零次方的定义:
数的零次方是指这个数连乘0次的结果。根据数学规定,任何非零数的零次方都等于1。
2.零次方的推导:
可以通过数学运算法则来推导出任何数的零次方等于1。设a表示一个非零数,那么a的零次方可以表示为a^0。根据指数的乘法法则,a^0=a^(1-1)=a^1*a^(-1)。
而根据指数的倒数法则,a^(-1)等于a除以a自身,即a^(-1)=1/a。因此,a^0=a*(1/a)=1。所以,任何非零数的零次方都等于1。

3.零次方的应用:
3.1在数学中,零次方的概念经常用于简化计算和推导公式,特别是在指数运算和级数展开、方程求解等方面。
3.2在物理学和工程学中,零次方的概念也有一些应用。例如,在电路分析中,将电流或电压的幅值取为常数时,可以将其视为零次方。
拓展知识:
零次方的数学证明:通过数学的归纳法,可以进一步证明任何非零数的零次方等于1。首先,对于任意非零数a,a^1=a,这是指数的定义。然后,假设对于任意非零数a,a^n=1成立,其中n是一个正整数。
在归纳步骤中,我们考虑a的n+1次方,即a^(n+1)=a^n*a。由归纳假设可知,a^n=1,所以a^(n+1)=1*a=a。因此,根据归纳法,任何非零数的零次方等于1。
零次方的性质:
对于非零数a,a^0=1。对于0这个特殊的数,0^0是没有确定值的,因为0没有唯一的倒数。
零次方的应用误区:
有时候,在一些复杂的数学问题中,出现0^0的情况。但是,0^0并不是一个明确的数值,因此在具体问题中需要根据具体情况进行讨论和分析,不能简单地将其视为1或0。
以上就是关于任何数的0次幂是多少,任何数的0次幂都等于1的全部内容,以及任何数的0次幂是多少的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。