导数定义中x增量必须大于0吗？
导数定义中x增量不必须大于0。
根据导数的定义可知，定义中把x增量取的是大于零的，定义给出的取值只是为了方便我们理解导数的定义，定义中的x增量也可以认为是小于零的，但是必须是在x的邻域范围之内，这样一来所得到的求导公式就会和x增量大于零是有所差别，而且在判断函数增减性时也会不同。
高中导数的定义及几何意义
高中导数的定义
导数定义
一、导数第一定义
设函数 y = f(x) 在点 x0 的某个邻域内有定义当自变量x 在 x0 处有增量△x ( x0 + △x 也在该邻域内 ) 时相应地函数取得增量 △y = f(x0 + △x) - f(x0) 如果 △y 与 △x 之比当 △x→0 时极限存在则称函数 y = f(x) 在点 x0 处可导并称这个极限值为函数 y = f(x) 在点 x0 处的导数记为 f'(x0) ,即导数第一定义
二、导数第二定义
设函数 y = f(x) 在点 x0 的某个邻域内有定义当自变量x 在 x0 处有变化 △x ( x - x0 也在该邻域内 ) 时相应地函数变化 △y = f(x) - f(x0) 如果 △y 与 △x 之比当 △x→0 时极限存在则称函数 y = f(x) 在点 x0 处可导并称这个极限值为函数 y = f(x) 在点 x0 处的导数记为 f'(x0) ,即导数第二定义
三、导函数与导数
如果函数 y = f(x) 在开区间I内每一点都可导就称函数f(x)在区间 I 内可导。这时函数 y = f(x) 对于区间 I 内的每一个确定的 x 值都对应着一个确定的导数这就构成一个新的函数称这个函数为原来函数 y = f(x) 的导函数记作 y', f'(x), dy/dx, df(x)/dx。导函数简称导数。
导数（Derivative）是微积分中的重要基础概念。当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。一个函数存在导数时，称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。导数实质上就是一个求极限的过程，导数的四则运算法则来源于极限的四则运算法则。
右上图为函数 y = ƒ(x) 的图象，函数在x_0处的导数ƒ′(x_0) = lim{Δx→0} [ƒ(x_0 + Δx) - ƒ(x_0)] / Δx。如果函数在连续区间上可导，则函数在这个区间上存在导函数，记作ƒ′(x)或 dy / dx。
函数单调递增一阶导数一定大于零吗
导数大于零一定单调递增。
导数大于零一定在定义域上单调递增。但是函数单调递增并不可以推出导数大于零，因为导数要求原函数是在定义域上为连续的函数，导数大于零是函数单调递增的充分不必要条件。
单调递增函数求解方法
1、定义法
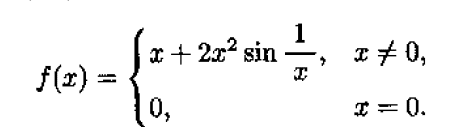
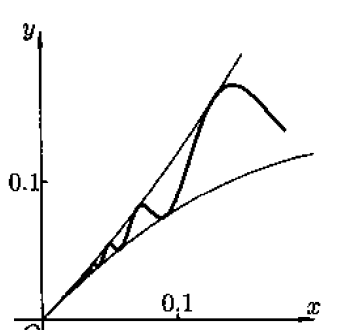
（）设x1、x2∈给定区间，且x1 （）计算f(x1)- f(x2)至最简。 （）判断上述差的符号。 2、求导法 利用导数公式进行求导，然后判断导函数和0的大小关系，从而判断增减性，导函数值大于0，说明是增函数，导函数值小于0，说明是减函数，前提是原函数必须是连续且可导的。 不是。 导数大于 0， 函数递增； 但函数递增，导数不一定存在。故不是充要条件。 例如分段函数 f(x) = x, x <0; f(x) = 2x, x ≥ 0. 在 x = 0 处连续，且函数递增。 但在 x = 0 处导数不存在。 函数在某一点的导数大于0，并不能保证函数在该点的某个邻域内单增，例如以下反例： 它在x=0处的导数大于0，但在x=0的任何邻域内都不单调，函数图象如下： 事实上，函数在一点x0处的导数大于0，只能保证在x0的某个邻域内f(x)>f(x0)，并不能保证在某个邻域内f'(x)>0，本质上是因为导函数在该点不一定不连续，从而导致导函数不一定不具有保号性。 以上就是关于导数定义中x增量必须大于0，高中导数的定义及几何意义的全部内容，以及导数定义中x增量必须大于0吗？的相关内容,希望能够帮到您。 版权声明：本文来自用户投稿，不代表【易百科】立场，本平台所发表的文章、图片属于原权利人所有，因客观原因，或会存在不当使用的情况，非恶意侵犯原权利人相关权益，敬请相关权利人谅解并与我们联系（邮箱：350149276@qq.com）我们将及时处理，共同维护良好的网络创作环境。想知道自己是不是抑郁了看什么科
凹函数的二阶导数一定大于0吗
