双曲线弦长公式是什么
设直线y=kx+b与双曲线交于A(x1,y1),B(x2,y2)两点,则|AB|=√(1+k?)[(X1+X2)?-4X1X2]。
在数学中,双曲线是定义为平面交截直角圆锥面的两半的一类圆锥曲线。它还可以定义为与两个固定的点(叫做焦点)的距离差是常数的点的轨迹。这个固定的距离差是a的两倍,这里的a是从双曲线的中心到双曲线最近的分支的顶点的距离。a还叫做双曲线的半实轴。
双曲线的弦长是指什么?
指直线与圆锥曲线相交所得弦长d。
弦长公式:d=√(1+k2)|x1-x2|
=√[(1+k2)(x1-x2)2]
=√(1+1/k2)|y1-y2|
=√[(1+1/k2)(y1-y2)2]
扩展资料
推导如下:
由直线的斜率公式:k=(y1-y2)/(x1-x2)
得y1-y2=k(x1-x2)或x1-x2=(y1-y2)/k
分别代入两点间的距离公式:|AB|=√[(x1-x2)2;+(y1-y2)2;]
稍加整理即得:
|AB|=|x1-x2|√(1+k2;)或|AB|=|y1-y2|√(1+1/k2;)
·双曲线的标准公式与反比例函数
X2/a2-Y2/b2=1(a>0,b>0)
而反比例函数的标准型是xy=c(c≠0)
但是反比例函数图像确实是双曲线轨迹经过旋转得到的
因为xy=c的对称轴是y=x,y=-x而X2/a2-Y2/b2=1的对称轴是x轴,y轴
所以应该旋转45°
设旋转的角度为a(a≠0,顺时针)
(a为双曲线渐近线的倾斜角)
则有:X=xcosa+ysina
Y=-xsina+ycosa
取a=π/4
则:
X2-Y2=(xcos(π/4)+ysin(π/4))2-(xsin(π/4)-ycos(π/4))2
=(√2/2x+√2/2y)2-(√2/2x-√2/2y)2
=4(√2/2x)(√2/2y)
=2xy
而xy=c
所以:
X2/(2c)-Y2/(2c)=1(c>0)
Y2/(-2c)-X2/(-2c)=1(c<0)
由此证的,反比例函数其实就是双曲线的一种形式,只不过是双曲线在平面直角坐标系内的另一种摆放形式。
双曲线弦长公式推导过程
(引):由直线的斜率公式:k
=
(y1
-
y2)
/
(x1
-
x2)
得y1
-
y2
=
k(x1
-
x2)
或
x1
-
x2
=
(y1
-
y2)/k
分别代入两点间的距离公式:|AB|
=
√[(x1
-
x2)??
+
(y1
-
y2)??
]
稍加整理即得:
|AB|
=
|x1
-
x2|√(1
+
k??)
或
|AB|
=
|y1
-
y2|√(1
+
1/k??)
双曲线的弦长公式是什么
公式是:设直线y=kx+b与双曲线交于A(x1,y1),B(x2,y2)两点,则|AB|=√(1+k²)[(X1+X2)²-4X1X2]。
在数学中,双曲线是定义为平面交截直角圆锥面的两半的一类圆锥曲线。它还可以定义为与两个固定的点(叫做焦点)的距离差是常数的点的轨迹。这个固定的距离差是a的两倍,这里的a是从双曲线的中心到双曲线最近的分支的顶点的距离。a还叫做双曲线的半实轴。
双曲线出现在许多方面:
作为在笛卡尔平面中表示函数的曲线;作为日后的阴影的路径;作为开放轨道(与闭合的椭圆轨道不同)的形状,例如在行星的重力辅助摆动期间航天器的轨道,或更一般地,超过最近行星的逃逸速度的任何航天器。
作为一个单一的彗星(一个旅行太快无法回到太阳系)的路径;作为亚原子粒子的散射轨迹(以排斥而不是吸引力作用,但原理是相同的);在无线电导航中,当距离到两点之间的距离而不是距离本身可以确定时等等。
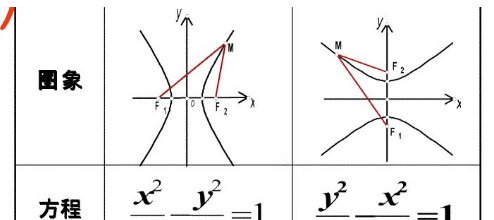
双曲线的每个分支具有从双曲线的中心进一步延伸的更直(较低曲率)的两个臂。对角线对面的手臂,一个从每个分支,倾向于一个共同的线,称为这两个臂的渐近线。所以有两个渐近线,其交点位于双曲线的对称中心,这可以被认为是每个分支反射以形成另一个分支的镜像点。
双曲线焦点弦长公式
双曲线焦点弦长公式:L=2a±2ex。弦长为连接圆上任意两点的线段的长度。弦长公式,在这里指直线与圆锥曲线相交所得弦长的公式。圆锥曲线,是数学、几何学中通过平切圆锥(严格为一个正圆锥面和一个平面完整相切)得到的一些曲线,如:椭圆,双曲线,抛物线等。
一般的,双曲线是定义为平面交截直角圆锥面的两半的一类圆锥曲线。它还可以定义为与两个固定的点(叫做焦点)的距离差是常数的点的轨迹。这个固定的距离差是a的两倍,这里的a是从双曲线的中心到双曲线最近的分支的顶点的距离。a还叫做双曲线的实半轴。焦点位于贯穿轴上,它们的中间点叫做中心,中心一般位于原点处。
以上就是关于双曲线弦长公式是什么,双曲线的弦长是指什么?的全部内容,以及双曲线弦长公式是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。