分式的除法法则是什么
分式除法法则是分式的运算法则,指分式除以分式,把除式的分子、分母颠倒位置与被除式相乘。
分式除以整式,可用整式乘分母或用整式除分子。
整式或分式除以分式,应把除式的分子、分母颠倒位置后与被除式相乘。
分式乘除法要注意符号法则,两数相乘,同号得正,异号得负,多个因式相乘,若负因数个数为奇数,则积为负;若负因数个数为偶数,则积为正,分式乘除的结果必须化成最简分式,在进行分式乘除混合运算时,同样要注意运算顺序。
分式的运算法则是什么,分式运算有哪些技巧
分数的运算法则:
1.分数的加减法则:同分母的分数相加减,只把分子相加减,分母不变。异分母的分数相加减,先通分,然后再加减。
2.分数乘整数法则:用分数的分子和整数相乘的积作分子,分母不变。
3.分数乘分数法则:用分子相乘的积作分子,分母相乘的积作为分母。
4.分数除以整数(0除外),等于分数乘以这个整数的倒数。
5.一个数除以分数,等于这个数乘以分数的倒数。
6.分数计算到最后,得数必须化成最简分数。
7.分数的基本性质:分数的分子和分母同时乘以或除以同一个数(0除外),分数的大小不变。
拓展资料:
一般地,如果A、B(B不等于零)表示两个整式,且B中含有字母,那么式子A / B 就叫做分式,其中A称为分子,B称为分母。分式是不同于整式的一类代数式,分式的值随分式中字母取值的变化而变化。
定义
形如
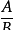
(A、B是整式,B中含有字母)的式子叫做分式。其中A叫做分式的分子,B叫做分式的分母。当分式的分子的次数低于分母的次数时,我们把这个分式叫做真分式;当分式的分子的次数高于分母的次数时,我们把这个分式叫做假分式。
注意:判断一个式子是否是分式,不要看式子是否是
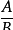
的形式,关键要满足:分式的分母中必须含有字母,分子分母均为整式。无需考虑该分式是否有意义,即分母是否为零。由于字母可以表示不同的数,所以分式比分数更具有一般性。
方法:数看结果,式看形。
分式条件
分式有意义条件:分母不为0。
2.分式值为0条件:分子为0且分母不为0。
3.分式值为正(负)数条件:分子分母同号得正,异号得负。
4.分式值为1的条件:分子=分母≠0。
5.分式值为-1的条件:分子分母互为相反数,且都不为0。
代数式分类
整式和分式统称为有理式。
带有根号且根号下含有字母的式子叫做无理式。
无理式和有理式统称代数式。
分式除法公式运算法则
分数除法是分数乘法的逆运算。分数除法的计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数。当除数小于1,商大于被除数;当除数等于1,商等于被除数;当除数大于1,商小于被除数。被除数乘除数的倒数能约分的要约分。
分数除法法则:分数甲除以分数乙就是分数甲乘以分数乙的倒数。a/b÷c/d=a/b×d/c
分式的运算法则公式
乘法:把分子相乘的积作为积的分子,把分母相乘的积作为积的分母。

除法:除以一个分式等于乘以这个分式的倒数。
加减法:同分母分式相加减,分母不变,把分子相加减。异分母的分式先通分,化为同分母的分式,再加减。
分式方程:分母中含有未知数的方程叫分式方程。使方程的分母为0的解称为原方程的增根。

答案如图所示

分式的除法
分式除法法则分式的运算法则之一分式的除法法则是:

1.分式除以整式,可用整式乘分母或用整式除分子。
2.整式或分式除以分式,应把除式的分子、分母颠倒位置后与被除式相乘。
在分数除法中,除以一个数,等于乘以这个数的倒数。在分式除法中,也可以这样计算。分式除法在计算的时候,我们把除式的分子和分母倒过来,再与被除式相乘,所以,b/a除以d/c,就等于b/a乘以c/d,等于bc/ad。当分式除以整式时,分子则不用作任何变化,只需把分母与这个整式相乘出来的乘积,作为分式的分母。如:a/b除以c,可以写作a/bc。

以上就是关于分式的除法法则是什么的全部内容,以及分式的除法法则是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。