n的x次方的导数是什么
n的x次方的导数:
y=x^n。
取对数:lny=n·lnx。
两边同时取微分:dlny=n·dlnx。
变形:(1/x)dy=n(1/x)dx。
dy/dx=ny/x。
将y=x^n代入上式,dy/dx=n(x^n)/x=nx^(n-1)。
导数(Derivative)是微积分中的重要基础概念。当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。一个函数存在导数时,称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。导数实质上就是一个求极限的过程,导数的四则运算法则来源于极限的四则运算法则。
x^n导数怎么
(x^n)'=nx^n-1。(x^n)'=nx^n-1是一个公式。
当N大于0等于Xn,当N等于0等于1,当N小于0等于X的n绝对值方分之1。
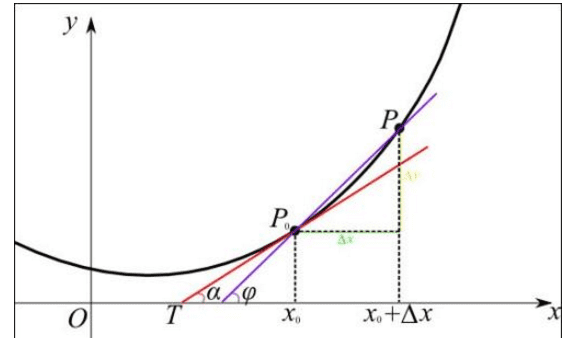
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。
不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
常用导数公式:
1.y=c(c为常数)y'=0。
2.y=x^n y'=nx^(n-1)。
3.y=a^x y'=a^xlna,y=e^x y'=e^x。
4.y=logax y'=logae/x,y=lnx y'=1/x。
5.y=sinx y'=cosx。
6.y=cosx y'=-sinx。
x的n次方导
用高中学的知识,是对x²、x³求导,找出规律来的,但是不能验证成立,严格推导的话需要用到的知识高中还接触不到的,我写出来你看看好了.
y=x^n
取对数:lny = n·lnx
两边同时取微分:dlny = n·dlnx
变形:(1/x)dy = n(1/x)dx
dy/dx = ny/x
将y=x^n代入上式,dy/dx = n(x^n)/x = nx^(n-1)
n阶导数公式都有哪些
考研常用的n阶导数公式:1、幂函数。2、指数函数。3、对数函数。4、三角函数。
1、幂函数: 若 f(x) = x^n,其中 n 为正整数,则 f^(n)(x) = n!,其中 n! 表示 n 的阶乘。幂函数是一种常见的数学函数,其定义形式为 f(x) = x^n,其中 x 是自变量,n 是指数。幂函数描述了一个变量与自身连乘多次的关系。
2、指数函数:若 f(x) = e^x,则 f^(n)(x) = e^x。指数函数是一种常见的数学函数,其定义形式为 f(x) = a^x,其中 a 是底数,x 是指数。指数函数描述了指数的幂运算关系。指数函数的性质和行为与底数 a 的取值相关。

3、对数函数:若 f(x) = ln(x),则 f^(n)(x) = (-1)^(n-1) * (n-1)! / x^n,其中 n ≥ 1。对数函数是一种常见的数学函数,其定义形式为 f(x) = logₐ(x),其中 a 是底数,x 是变量。对数函数描述了底数为 a 的对数运算关系。
4、三角函数:若 f(x) = sin(x),则 f^(n)(x) = sin(x + (n-1) * π/2),其中 n 为正整数。若 f(x) = cos(x),则 f^(n)(x) = cos(x + n * π/2),其中 n 为非负整数。三角函数在数学中有广泛的应用,尤其在几何学、三角学、物理学、工程学等领域中的角度、周期性和波动性等问题中起着重要的作用。
n阶倒数含义
1、n阶导数是指函数的n次导数,表示对函数进行n次求导的结果。n阶导数描述了函数在该点的高阶变化率。n阶导数表示了函数在特定点处的曲率、凹凸性以及更高阶的变化特性。例如,二阶导数可以用来判断函数的拐点位置,正值表示函数凸向上,负值表示函数凸向下,零值表示函数可能存在拐点。

2、具体地,给定函数 f(x),它的n阶导数可以通过连续地对函数进行求导 n 次得到。第一阶导数是函数 f(x) 的一阶导数,常表示为 f'(x) 或 df(x)/dx。第二阶导数是函数的二阶导数,常表示为 f''(x) 或 d²f(x)/dx²;第 n 阶导数常表示为 f⁽ⁿ⁾(x) 或 dⁿf(x)/dxⁿ。
3、在应用中,n阶导数在微积分、物理学、工程学和经济学等领域中具有重要的意义,可以用于解决最优化问题、描述物理系统的变化、分析函数的性质等。n阶导数在物理学中可以代表某种物理量的变化速率。比如,二阶导数代表了物体的加速度,表示速度的变化率。
以上就是关于xn导数怎么,n的x次方的导数是什么的全部内容,以及n的x次方的导数是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。