什么的平行四边形是矩形
平行四边形是在同一个二维平面内,由两组平行线段组成的闭合图形,在欧几里德几何中,平行四边形是具有两对平行边的简单(非自相交)四边形。
平行四边形一般用图形名称加四个顶点依次命名。
其相对或相对的侧面具有相同的长度,并且平行四边形的相反的角度是相等的。
平行四边形不是轴对称图形,但平行四边形是中心对称图形。
矩形和菱形是轴对称图形。
注:正方形,矩形以及菱形也是一种特殊的平行四边形,三者具有平行四边形的性质。
矩形的定义
矩形也叫长方形,是有一个内角是直角的平行四边形。
在几何学科定义中,矩形为四个内角相等的四边形,即是说所有内角均为直角。
判定:
矩形的常见判定方法如下:
(1)有一个角是直角的平行四边形是矩形;
(2)对角线相等的平行四边形是矩形;
(3)有三个角是直角的四边形是矩形;
(4)定理:经过证明,在同一平面内,任意两角是直角,任意一组对边相等的四边形是矩形;
(5)对角线相等且互相平分的四边形是矩形。
判定应用:
例1:如下图,已知ABCD的对角线AC和BD相交于点O,△AOB是等边三角形,AB=4.求这个平行四边形的面积。
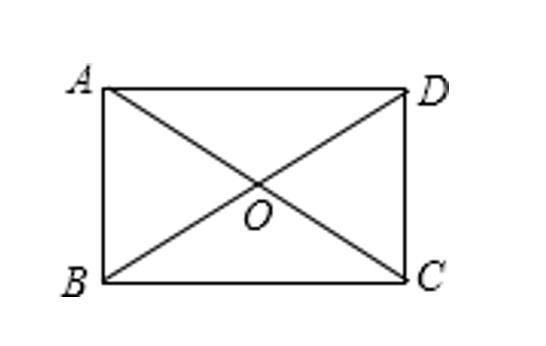
分析:首先根据△AOB是等边三角形及平行四边形对角线互相平分的性质判定出ABCD是矩形,再利用勾股定理计算边长,从而得到面积。
例2:已知:如下图,在ABCD中,M为BC中点,∠MAD=∠MDA.求证:四边形ABCD是矩形。
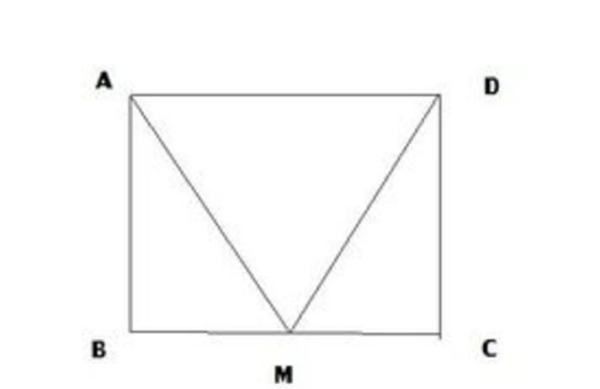
分析:根据定义去证明一个角是直角,由△ABM≌DCM(SSS)即可实现。
证明:
因为平行四边形ABCD
故:AB=CD,AB‖CD
故:∠B+∠D=180度
因为M是BC中点
故:BM=MC
因为∠MAD=∠MDA
故:MA=MD
故:△MAB≌△MDC(SSS)
故:∠B=∠D=90度
故:四边形ABCD是矩形(有一个内角为90度的平行四边形是矩形)
例3:已知:如下图,ABCD的四个内角平分线相交于点E,F,G,H.求证:EG=FH。
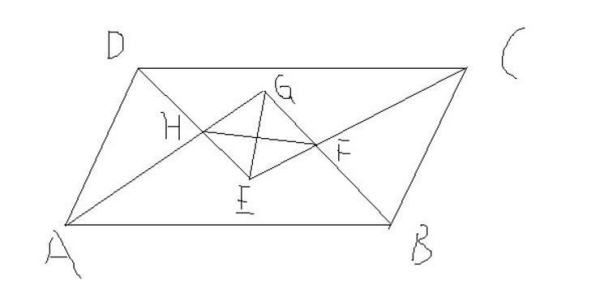
分析:要证的EG,FH为四边形EFGH的对角线,因此只需证明四边形EFGH为矩形,可选用“三个角是直角的四边形是矩形”来证明。
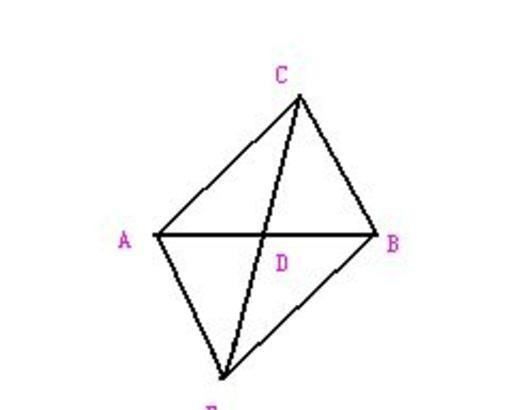
例4:已知:如下图,在△ABC中,∠C= 90°,CD为中线,延长CD到点E,使得DE=CD,连结AE,BE,则四边形ACBE为矩形。
平行四边形是矩形的一种吗
不是。平行四边形判定是矩形是有条件的,有一个角为直角的平行四边形是矩形。矩形是有一组相邻边,相互垂直的平行四边形。矩形包括长方形和正方形,矩形属于特殊的平行四边形。
矩形的判定
1.有三个角是直角的四边形是矩形;
2.对角线互相平分且相等的四边形是矩形;
3.有一个角为直角的平行四边形是矩形;
4.对角线相等的平行四边形是矩形。
矩形的性质
1.矩形的4个角都是直角;
2.矩形的对角线相等且互相平分;
3.矩形所在平面内任一点到其两对角线端点的距离的平方和相等;
4.矩形既是轴对称图形,也是中心对称图形(对称轴是任何一组对边中点的连线),它至少有两条对称轴;
5.矩形具有平行四边形的所有性质。
矩形是特殊的平行四边形,特殊在哪
矩形是特殊的平行四边形。
矩形是一种四边形,其中四个角度相等且四个边长度相等。矩形的四个角度均为90度,这也是为什么矩形又被称为“正方形”的原因。矩形是平面图形中最基本的图形之一,其面积、周长等计算公式较为简单,常用于基础几何学的学习和研究中。
在矩形中,可以根据不同的分类方法进行分类。根据边长和角度的关系,可以将矩形分为普通矩形和等边矩形。普通矩形的长和宽不一定相等,其对角线长度也不一定相等。而等边矩形的长、宽和对角线长度均相等,其对角线长度为边长的根号2倍。
在矩形中,有许多的性质和定理。例如,矩形的对角线平分一组对角;矩形对角线相等且平分;矩形内角平分线分对边成等长;矩形的对角线垂直平分等等。这些性质和定理是解决几何问题的基础,对于理解和掌握几何知识有着重要的意义。
在实际应用中,矩形也有着广泛的应用。例如,矩形的面积和周长计算是建筑设计、计算物体运动等领域的基础;矩形对角线的长度计算是电路设计、计算图像中两点距离等领域的基础;矩形的内角平分线计算是光学、三角函数等领域的基础。

矩形的常见判定方法:
1、有一个角是直角的平行四边形是矩形。
2、对角线相等的平行四边形是矩形。
3、有三个角是直角的四边形是矩形。
4、定理:经过证明,在同一平面内,任意两角是直角,任意一组对边相等的四边形是矩形。
5、对角线相等且互相平分的四边形是矩形。
以上就是关于矩形的定义,什么的平行四边形是矩形的全部内容,以及什么的平行四边形是矩形的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。