正弦函数的周期怎么求
求正弦函数的周期的方法:若y=Asin(ωx+φ)+b的周期T=2π/│ω│,若y=│Asin(ωx+φ)+b│时当b=0时,T=π/│ω│;当b≠0时,T=2π/│ω│。
正弦型函数解析式:y=Asin(ωx+φ)+h;各常数值对函数图像的影响:
φ(初相位):决定波形与X轴位置关系或横向移动距离(左加右减)。
ω:决定周期(最小正周期T=2π/|ω|)。
A:决定峰值(即纵向拉伸压缩的倍数)。
h:表示波形在Y轴的位置关系或纵向移动距离(上加下减)。
正弦函数周期公式
t=2π/w公式是正弦函数周期公式。
T是指周期;W是指角速度,也叫角频率。函数的周期性定义:若存在一非零常数T,对于定义域内的任意x,使f(x)=f(x+T)恒成立,则f(x)叫做周期函数,T叫做这个函数的一个周期。
函数周期性的关键的几个字“有规律地重复出现”。当自变量增大任意实数时(自变量有意义),函数值有规律的重复出现。假如函数f(x)=f(x+T)(或f(x+a)=f(x-b)其中a+b=T),则说T是函数的一个周期,T的整数倍也是函数的一个周期。
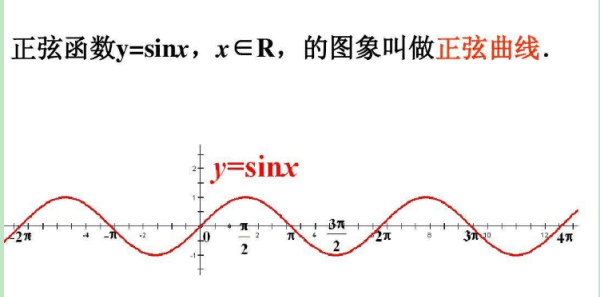
正弦型函数简介
正弦型函数是形如y=Asin(ωx+φ)+k的函数,其中A,ω,φ,k是常数,且ω≠0。函数y=Asin(ωx+φ),(A>0,ω>0),x∈R的图象可以看作是用下面的方法得到的:先把y=sinx的图象上所有的点向左(φ>0)或向右(φ<0)平行移动|φ|个单位。
再把所得各点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的1/ω倍(纵坐标不变),再把所得各点的纵坐标伸长(A>1)或缩短(00,ω>0),x∈〔0,+∞)表示一个振动量时,A就表示这个量振动时离开平衡位置的最大距离,通常把它叫做振动的振幅。
往复振动一次所需要的时间T=2π/ω,它叫做振动的周期。单位时间内往复振动的次数f=1/T=ω/2π,它叫做振动的频率,ωx+φ叫做相位,φ叫做初相(即当x=0时的相位)。
正弦函数的周期怎么算?
正弦函数是一种周期函数,其周期可以通过以下公式来计算:
周期T = 2π/ω
其中,ω是正弦函数的角频率,定义为每单位时间内完整周期的弧度数。对于一般的正弦函数y = A*sin(ωx + φ),其中A是振幅,φ是相位,可以通过观察函数的图像或根据具体问题来确定角频率ω。
值得注意的是,角频率ω与频率f之间存在关系,即ω = 2πf。频率表示正弦函数每秒钟重复周期的次数。因此,周期T也可以通过频率f来计算:
周期T = 1/f
对于常见的正弦函数,如y = sin(x)或y = cos(x),它们的周期均为2π。
正弦函数的周期怎么算?
正弦函数的周期可以通过以下方式计算:
对于一般形式的正弦函数 y = A * sin(Bx + C) + D,其中 A、B、C 和 D 是常数。
1. 如果 B 是一个整数:则正弦函数的周期为 2π/B。即正弦函数在每个 2π/B 的间隔内重复一次。
2. 如果 B 是一个分数:则正弦函数的周期为 2π/(B的绝对值)。即正弦函数在每个 2π/(B的绝对值) 的间隔内重复一次。
需要注意的是,A、C 和 D 不会影响正弦函数的周期,它们只会影响函数的振幅、平移和垂直方向的平移。
举例来说,如果有正弦函数 y = 3 * sin(2x + π/4) + 2,则其周期为 2π/2 = π。这意味着正弦函数在每个 π 的间隔内重复一次。
正弦函数的周期怎么算
与一个角的终边相同的角用2kπ,终边在一条直线上的就用kπ。
①如果求单调区间的话
比如f(x)=sin(2x+π/3)求单调增区间
那就是2kπ
因为一个周期里面含有一个单增区间或单减区间。
所以有-π/2+2kπ<2x+π/3<π/2+2kπ
-5π/12+kπ<x<π/12+kπ
②如果求对称轴的话
因为每个周期里面含有2个对称轴
所以是kπ
所以有2x+π/3=π/2+kπ
x=π/12+kπ/2
同理求对称中心
就令2x+π/3=kπ
x=-π/6+kπ/2
③可能还会用到角度的问题
与一个角的终边相同的角用2kπ
终边在一条直线上的就用kπ
简介:
正弦(sine),数学术语,在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA(由英语sine一词简写得来),即sinA=∠A的对边/斜边。
古代说法,正弦是股与弦的比例。
以上就是关于正弦函数周期公式,正弦函数的周期怎么的全部内容,以及正弦函数的周期怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。