立体几何中的向量方法知识点
ab向量除以ab向量的模应该AB方向的单位向量,ab向量除以ab向量的模应该一个向量,既包含方向,又包含大小。其中大小又叫向量的模或长度,向量的模仅是向量的大小或长度。
在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
空间向量与立体几何知识点
空间向量与立体几何知识点:
共线向量:如果表示空间向量的有向线段所在的直线平行或重合,这些向量也叫作共线向量或平行向量,a平行于b,记作b//a。
共线向量定理:空间任意两个向量a、b(b≠0),a//b,存在实数λ,使a=λb。
空间向量的概念:在空间,把具有大小和方向的量叫作向量,向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量。向量具有平移不变性。
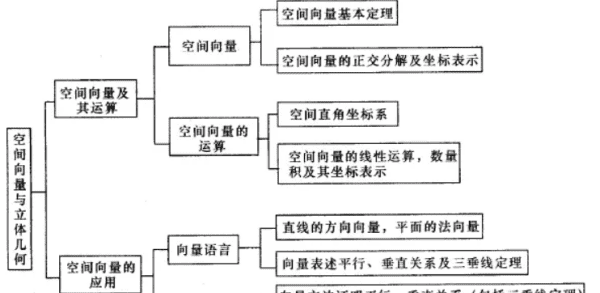
基本定理
1、共线向量定理两个空间向量a,b向量(b向量不等于0),a//b的充要条件是存在唯一的实数λ,使a=λb。
2、共面向量定理:如果两个向量a,b不共线,则向量c与向量a,b共面的充要条件是:存在唯一的一对实数x,y,使c=ax+by。
3、空间向量分解定理:如果三个向量a、b、c不共面,那么对空间任一向量p,存在一个唯一的有序实数组x,y,z,使p=xa+yb+zc,任意不共面的三个向量都可作为空间的一个基底,零向量的表示唯一。
立体几何法向量简便算法
立体几何求面的法向量的方法是:
1、在图中找到垂直与面的向量;
2、如果找不到,就设向量n等于x,y,z,因为法向量垂直于面,所以向量n垂直于面内两相交直线可列出两个方程,三个未知数,然后根据计算,取z或x或y等于一个数,求出面的一个法向量;
会求法向量后
1、二面角的求法就是求出两个面的法向量,可以求出两个法向量的夹角为两向量的数量积除以两向量模的乘积,过在两面的同一边可以看到两向量的箭头或箭尾相交,那么二面角就是上面求的两法向量的夹角的补角,如果只能看到其中一个的箭头和另一个的箭尾相交,那么上面两向量的夹角就是所求;
2、点到平面的距离就是求出该面的法向量,在平面上任取一点除平面外那点在平面内的射影,求出平面外那点和你所取的那点所构成的向量记为n1,点到平面的距离就是法向量与n1的数量积的绝对值除以法向量的模即得所求。
立体几何中的向量方法教案
同底同高的三棱锥是三棱柱体积的1/3。这一个结果来自“祖衡定理”(祖衡是
祖冲之的孙子。南北朝时代大数学家)“两个物体用平行于一个固定平面的平面
去截。如果每次所截的两个截面面积都相等。则这两个物体体积相等。”(没有
初等方法证明。用微积分,结果是显然的。)从而有。等底等高的掕锥等体积
(楼主试试用祖衡定理证明!)。然后,如图把三棱柱截成三个等体积的三棱
锥。即可完成证明.
V(B-ACA1 )=V(B-A1CC1)[底:S⊿ACA1=S⊿A1CC1.同高]
V(A1-ABD)=V(A1-BB1C1)[等底同高]。
空间向量与立体几何知识点归纳
空间向量与立体几何知识点有:
1、以向量为载体,运用向量的线性运算尤其是数量积的应用、证明平行、垂直等问题,以各种题型,尤其以解答题为主进行考查,利用空间向量数量积求解相应几何问题,建立适当的空间直角坐标系,利用向量的坐标运算证明线线、线面、面面的平行于垂直,以及空间角与距离的求解问题,以解答题为主,多属于中档题。
2、利用向量数量积的有关知识解决几何问题,利用向量坐标运算考查平行、垂直、角、距离等几何问题是高考的热点。
基本定理
1、共线向量定理
两个空间向量a,b向量(b向量不等于0),a∥b的充要条件是存在唯一的实数λ,使a=λb。
2、共面向量定理
如果两个向量a,b不共线,则向量c与向量a,b共面的充要条件是:存在唯一的一对实数x,y,使c=ax+by。
3、空间向量分解定理
如果三个向量a、b、c不共面,那么对空间任一向量p,存在一个唯一的有序实数组x,y,z,使p=xa+yb+zc。
任意不共面的三个向量都可作为空间的一个基底,零向量的表示唯一。
以上就是关于空间向量与立体几何知识点,立体几何中的向量方法知识点的全部内容,以及立体几何中的向量方法知识点的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。