向量数乘运算及其几何意义导学案
向量是有大小和方向的,向量数乘运算的几何意义是把向量沿着原方向(用正数数乘向量)或反方向(用负数数乘向量)伸长或缩短,特别注意的是0数乘向量得到零向量。
在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小和方向的量。它可以形象化地表示为带箭头的线段。箭头所指代表向量的方向;线段长度代表向量的大小。与向量对应的只有大小,没有方向的量叫做数量(物理学中称标量)。
向量乘法运算及其几何意义
向量是由n个实数组成的一个n行1列(n×1)或一个1行n列(1×n)的有序数组;
向量的点乘,也叫向量的 内积、数量积 ,对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作,点乘的结果是一个 标量 。
对于向量 和向量 :
a和b的点积公式为:
注意:要求一维向量a和向量b的行列数相同。
点乘的几何意义是可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影,有公式:
推导过程如下,首先看一下向量组成:
定义向量:
根据三角形余弦定理有:
根据关系c=a-b(a、b、c均为向量)有:
即:
向量a,b的长度都是可以计算的已知量,从而有a和b间的夹角θ:
根据这个公式就可以计算向量a和向量b之间的夹角。从而就可以进一步判断这两个向量是否是同一方向,是否正交(也就是垂直)等方向关系,具体对应关系为:
方向基本相同,夹角在0°到90°之间
正交,相互垂直
方向基本相反,夹角在90°到180°之间
两个向量的叉乘,又叫向量积、外积、叉积,叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
对于向量a和向量b:
其中:
根据i、j、k间关系,有:
在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。
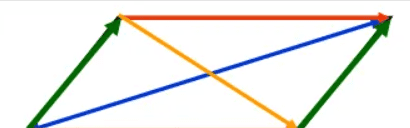
在3D图像学中,叉乘的概念非常有用,可以通过两个向量的叉乘,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。如下图所示:
在二维空间中,叉乘还有另外一个几何意义就是:a×b等于由向量a和向量b构成的平行四边形的面积。
向量数乘运算及其几何意义教案
向量数乘运算及其几何意义
向量是有大小和方向的。向量数乘运算的几何意义是:把向量沿着原方向(用正数数乘向量)或反方向(用负数数乘向量)伸长或缩短,特别注意的是0数乘向量得到零向量。
向量的数乘运算的定义:
1.定义:一般地,我们规定实数λ与向量a的积是一个向量
,这种运算叫做向量的数乘,记作λa.
2.规定:(1)|λa|=|λ||a|.(2)当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相反;当λ=0时,λa=0.
3.运算律:
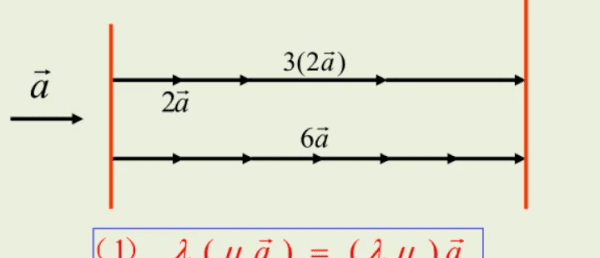
设λ,μ为实数,则(1)λ(μa)=λμa;
(2)(λ+μ)a=λa+μa;(3)λ(a+b)=λa+λb.
特别地,我们有
(-λ)a=-(λa)=λ(-a),λ(a-b)=λa-λb
向量的数乘运算
定义:一般我们规定实数λ与向量a的积是一个向量,这种运算叫做向量的数乘,记作λa。
运算规则:
(1)|λa|=|λ||a|.
(2)当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相反;当λ=0时,λa=0.
注意事项:
(1)λa中的实数λ叫做向量a的系数.
(2)向量数乘运算的几何意义是把a沿着a的方向或a的反方向扩大或缩小.
(3)当λ=0或a=0时,λa=.注意是0,而不是0.
向量相乘的几何意义
向量相乘的几何意义:表示一向量在另一向量上的射影乘以另一向量。
一、向量的介绍
在数学中,向量(也称为欧几里得向量、几何向量),指具有大小和方向的量。
二、向量的类型
单位向量:长度等于1个单位的向量。
平行向量(共线向量):方向相同或相反的非零向量。零向量与任一向量平行。

相等向量:长度相等且方向相同的向量。
三、数与向量的乘法满足的运算律
结合律:(λa)·b=λ(a·b)=(a·λb)。
向量对于数的分配律(第一分配律):(λ+μ)a=λa+μa。
数对于向量的分配律(第二分配律):λ(a+b)=λa+λb。
数乘向量的消去律:1、如果实数λ≠0且λa=λb,那么a=b。2、如果a≠0且λa=μa,那么λ=μ。

向量的表达方式
1、代数表示
一般印刷用黑体的小写英文字母(a、b、c等)来表示,手写用在a、b、c等字母上加一箭头(→)表示,也可以用大写字母AB、CD上加一箭头(→)等表示。
2、几何表示
向量可以用有向线段来表示。有向线段的长度表示向量的大小,向量的大小,也就是向量的长度。长度为0的向量叫做零向量,记作长度等于1个单位的向量,叫做单位向量。箭头所指的方向表示向量的方向。

3、坐标表示
在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i,j作为一组基底。a为平面直角坐标系内的任意向量,以坐标原点O为起点作向量OP=a。
由平面向量基本定理可知,有且只有一对实数(x,y),这就是向量a的坐标表示。其中(x,y)就是点P的坐标。向量OP称为点P的位置向量。
以上就是关于向量乘法运算及其几何意义,向量数乘运算及其几何意义导学案的全部内容,以及向量数乘运算及其几何意义导学案的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。