抛物线的切线方程怎么求
抛物线的切线方程是y“=2ax+b,切线方程是研究切线以及切线的斜率方程,涉及几何、代数、物理向量、量子力学等内容。是关于几何图形的切线坐标向量关系的研究,分析方法有向量法和解析法。
平面内,到定点与定直线的距离相等的点的轨迹叫做抛物线。其中定点叫抛物线的焦点,定直线叫抛物线的准线。当a与b同号时(即ab>0),对称轴在y轴左侧;因为若对称轴在左边则对称轴小于0,也就是-b/2a
当a与b异号时(即ab0,若要b/2a小于0,则a、b要异号
抛物线的切线方程怎么求
抛物线的切线方程是y'=2ax+b,切线方程是研究切线以及切线的斜率方程,涉及几何、代数、物理向量、量子力学等内容。是关于几何图形的切线坐标向量关系的研究,分析方法有向量法和解析法。
平面内,到定点与定直线的距离相等的点的轨迹叫做抛物线。其中定点叫抛物线的焦点,定直线叫抛物线的准线。当a与b同号时(即ab>0),对称轴在y轴左侧;因为若对称轴在左边则对称轴小于0,也就是-b/2a
抛物线切线方程
抛物线切线方程:
1、已知切点Q(x0,y0),若y²=2px,则切线y0y=p(x0+x);若x²=2py,则切线x0x=p(y0+y)等。
2、已知切点Q(x0,y0)
若y²=2px,则切线y0y=p(x0+x)。
若x²=2py,则切线x0x=p(y0+y)。
3、已知切线斜率k
若y²=2px,则切线y=kx+p/(2k)。
若x²=2py,则切线x=y/k+pk/2(y=kx-pk²/2)。
扩展资料:
性质
1、过抛物线焦弦两端的切线的交点在抛物线的准线上。
2、过抛物线焦弦两端的切线互相垂直。
3、以抛物线焦弦为直径的圆与抛物线的准线相切。
4、过抛物线焦弦两端的切线的交点与抛物线的焦点的连线和焦点弦互相垂直。
5、过焦弦两端的切线的交点与焦弦中点的连线,被抛物线所平分。
已知斜率求抛物线的切线方程
抛物线切线方程:
1、已知切点Q(x0,y0),若y²=2px,则切线y0y=p(x0+x);若x²=2py,则切线x0x=p(y0+y)等。
2、已知切点Q(x0,y0)
若y²=2px,则切线y0y=p(x0+x)。
若x²=2py,则切线x0x=p(y0+y)。
3、已知切线斜率k
若y²=2px,则切线y=kx+p/(2k)。
若x²=2py,则切线x=y/k+pk/2(y=kx-pk²/2)。

抛物线几何性质
(1)设抛物线上一点P的切线与准线相交于Q,F是抛物线的焦点,则PF⊥QF。且过P作PA垂直于准线,垂足为A,那么PQ平分∠APF。
(2)过抛物线上一点P作准线的垂线PA,则∠APF的平分线与抛物线切于P。从这条性质可以得出过抛物线上一点P作抛物线的切线的尺规作图方法。
(3)设抛物线上一点P(P不是顶点)的切线与法线分别交轴于A、B,则F为AB中点。这个性质可以推出抛物线的光学性质,即经焦点的光线经抛物线反射后的光线平行于抛物线的对称轴。各种探照灯、汽车灯即利用抛物线(面)的这个性质,让光源处在焦点处以发射出(准)平行光。
抛物线的切点弦方程怎么推导
抛物线切线方程:
1、已知切点Q(x0,y0),若y²=2px,则切线y0y=p(x0+x);若x²=2py,则切线x0x=p(y0+y)等。
2、已知切点Q(x0,y0)
若y²=2px,则切线y0y=p(x0+x)。
若x²=2py,则切线x0x=p(y0+y)。
3、已知切线斜率k
若y²=2px,则切线y=kx+p/(2k)。
若x²=2py,则切线x=y/k+pk/2(y=kx-pk²/2)。
抛物线性质若椭圆的方程为
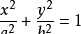
,点P
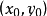
在椭圆上,则过点P椭圆的切线方程为
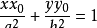
证明:
椭圆为
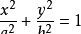
,切点为
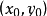
,则
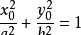
对椭圆求导得
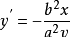
, 即切线斜率
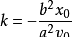
,故切线方程是
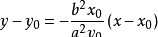
,将(1)代入并化简得切线方程为
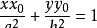
。
若双曲线的方程为
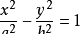
,点P
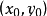
。
在双曲线上,则过点P双曲线的切线方程为
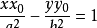
此命题的证明方法与椭圆的类似。
以上就是关于抛物线的切线方程怎么的全部内容,以及抛物线的切线方程怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。


