概率的估计值怎么样，概率论估计精度怎么算的

概率的估计值怎么样求

当样本数量足够多的时候概率的估计值近似等于频率，概率=事件发生次数/样本总数×100%。

概率，亦称“或然率”，它是反映随机事件出现的可能性大小。随机事件是指在相同条件下，可能出现也可能不出现的事件。例如，从一批有正品和次品的商品中，随意抽取一件，“抽得的是正品”就是一个随机事件。设对某一随机现象进行了n次试验与观察，其中A事件出现了m次，即其出现的频率为m/n。经过大量反复试验，常有m/n越来越接近于某个确定的常数。该常数即为事件A出现的概率，常用P(A)表示。

概率论估计精度怎么算的

概率论估计精度怎么算？当样本数量足够多的时候概率的估计值近似等于频率，概率=事件发生次数/样本总数×100%。

概率，亦称“或然率”，它是反映随机事件出现的可能性大小。随机事件是指在相同条件下，可能出现也可能不出现的事件。例如，从一批有正品和次品的商品中，随意抽取一件，“抽得的是正品”就是一个随机事件。设对某一随机现象进行了n次试验与观察，其中A事件出现了m次，即其出现的频率为m/n。经过大量反复试验，常有m/n越来越接近于某个确定的常数。该常数即为事件A出现的概率，常用P (A) 表示。

求一个事件的估计值。如果是估计发生的概率，那么就大量重复实验，样本容量趋于无穷时，频率趋近于概率。如果是估计参数，比如期望、方差等等。那么就用参数估计的公式。有矩法估计和极大似然估计两种方法。也可以大量重复实验，从而得到估计值。

已知概率密度函数求矩估计量

求矩估计量、矩估计值和极大似然估计值的详细过程：

1、根据题目给出的概率密度函数，计算总体的原点矩（如果只有一个参数只要计算一阶原点矩，如果有两个参数要计算一阶和二阶）。由于有参数这里得到的都是带有参数的式子。如果题目给的是某一个常见的分布，就直接列出相应的原点矩（E(x)）。

2、根据题目给出的样本。按照计算样本的原点矩，让总体的原点矩与样本的原点矩相等，解出参数。所得结果即为参数的矩估计值。

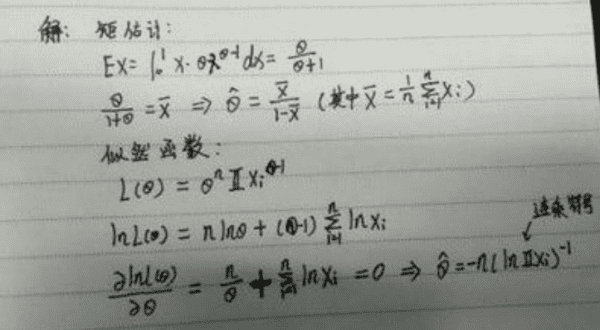
矩估计量的背景知识：

简单的讲，概率密度函数表示的就是随机变量X在某点的概率（所有点的概率和为1）。对于连续型的随机变量，其图像通常为一个连续的曲线，离散型的随机变量的图像一般是一个一个点组成。

“似然性”与“或然性”或“概率”意思相近，都是指某种事件发生的可能性，但是在统计学中，“似然性”和“或然性”或“概率”又有明确的区分。似然性则是用于在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。这里类似于“贝叶斯方法”的思路。

已知总体x的概率密度只有两种可能,设h0

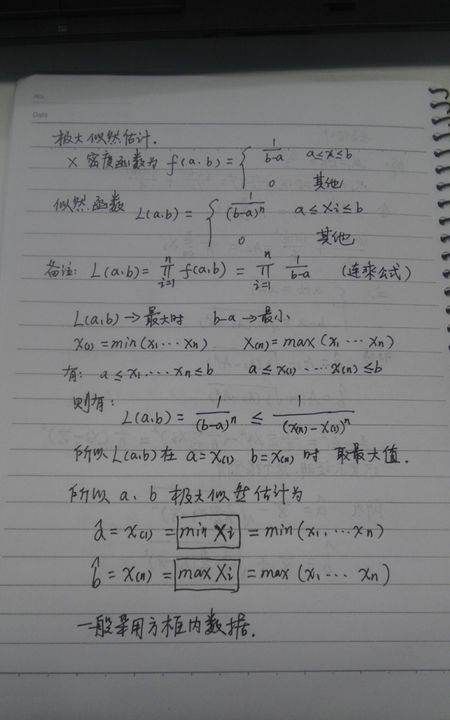
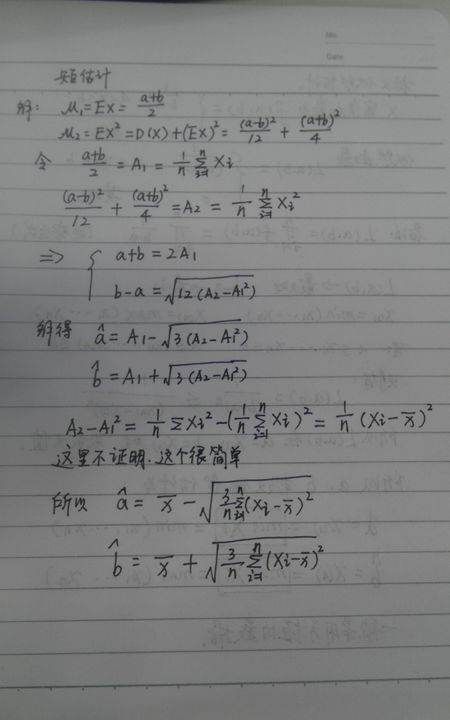
已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。

极大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

当然极大似然估计只是一种粗略的数学期望，要知道它的误差大小还要做区间估计。

扩展资料：

由最值原理，如果最值存在，此方程组求得的驻点即为所求的最值点，就可以很到参数的极大似然估计。极大似然估计法一般属于这种情况，所以可以直接按上述步骤求极大似然估计。

在寻找参数的矩法估计量时，对总体原点矩不存在的分布如柯西分布等不能用，另一方面它只涉及总体的一些数字特征，并未用到总体的分布。

因此矩法估计量实际上只集中了总体的部分信息，这样它在体现总体分布特征上往往性质较差，只有在样本容量n较大时，才能保障它的优良性,因而理论上讲，矩法估计是以大样本为应用对象的。

以上就是关于概率的估计值怎么样，概率论估计精度怎么算的的全部内容，以及概率的估计值怎么样求的相关内容,希望能够帮到您。